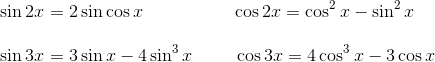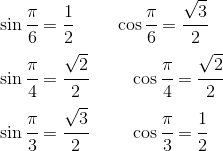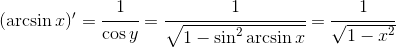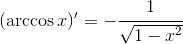原文作者：德夫林，斯坦福数学教授，英国数学科普作家。

译文作者：mathyrl，哆嗒数学网翻译组成员，软件工程师。

校对：333

 

 

微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文

新浪微博：http://weibo.com/duodaa

 

 

“每个人都会在某些方面表现优秀。”我们经常听到这样的论调，当有人因为在某件事情上表现不佳而感到沮丧时，通常可以从中得到安慰。特别地，父母们常常靠它来安慰自己的孩子们。然而很少有人认识到这个命题是可以用数学证明的。你只需要考虑200个本质上相互独立的人类行为表现特征，98%的人在至少其中一个特征上表现出众。这里“出众”定义为处于顶部或者底部的1%。（数学给出极值；如果你想有效保证处在顶部的1%，你需要更多的特征。这种现象是渐近的。）

这个结果源自于一个令人难以置信的但少有人知道的关于高阶超立方体的观察：随着维数的增加，内部点（即不在边界上）的比例无限制地缩小。

.
按照以下方法，你可以向你的孩子、爱人、学生、挚友、或者其他什么人，来证明他们---或是你自己，看情况而定---会在某方面表现优秀。
 

 

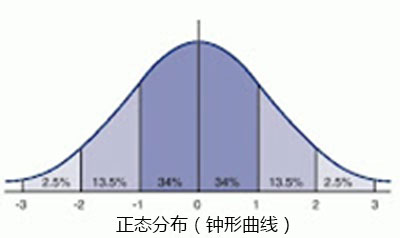
大家都熟悉钟形曲线（正态分布），它显示了在足够大的人口数量里对某一特征表现衡量的典型的分布。这个分布图形抓住了这样的事实：大多数人的得分聚集于一个“均值”附近，即中等值，只有极少数的人处在两端（特别差或者特别好）。

 

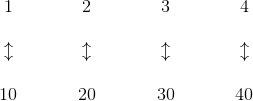
为了进行高维计算，我们先从一个几何上更简单的模型开始，即闭区间[0,100]，如图2所示。我们定义异常点为位于两端单位区间中的点。在这个模型里，对于单个的特征，只有2%的人是出众的，其余98%的人是“普通”的。
 

 

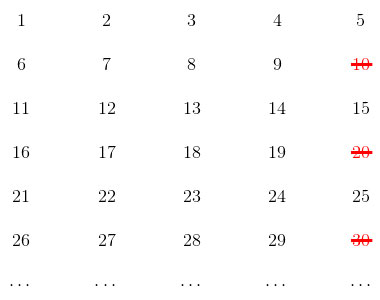
现在考虑2个特征，X和Y（按假设是相互独立的）。它们的分布可以被表示为一个100x100的正方形内含一个98x98的方块，如图3所示。

 

衡量一个人的特征X用x-坐标，特征Y用y-坐标。普通人被表示为内部正方形的点，出众者被表示为外围区域的点。

.
所有的点的总数是100×100。正常点的数目是98x98。所以异常点的数目是10000 – 9604 = 396。

因此异常点所占的比例是396/10000 = 0.0396，即3.96%。所以，当你考虑2个特征时，更多的人被归类为出众的（3.96%相对于2%）。

接下来看3个特征，X，Y，和Z，模型就变成一个100×100×100的立方体内含一个98×98×98的方体，如图4所示。

 

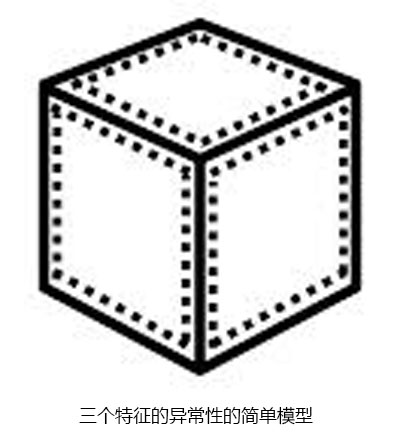
外部立方体的体积（表示总人口）是1000000。内部立方体的体积（表示普通人）是941192。所以外围区域的体积（表示出众者） = 1000000 – 941192 = 58808。因此出众者所占比例 = 58808/1000000 = 5.88%。

到目前为止，一切看起来都相当直接和合理。考虑超过3个特征，模型就是一个4维或更高维的超立方体，我们无法提供有意义的图像。但现在我们已经熟悉了这样的套路：模型把出众的人表示为1%的外壳里的点。为了看出这能导致什么，让我们直接跳到10个特征，X(1),…X(10)。那样的话，我们的模型就表示为一个100^10)体积的超立方体内含一个98^10体积的超立方体。(译者注：a^b表示a的b次方，下同)

外部超立方体的体积（~总人口）= 100^10，内部超立方体的体积（～普通人）= 98^10。因此，外围区域的体积（～出众者）= 100^10–98^10，出众者所占比例为(100^10–98^10)/ 100^10–98^10。现在，是时候搬出Wolfram Alpha(译者注：著名的数学引擎，擅长各种数学计算)来做计算了。算出结果为，对于10个特征，18.29%的人是出众的。

对于100个特征，X(1),…X(100)，我们的模型给出：超立方体的体积（～总人口）= 100^100。内部超立方体的体积（～普通人）= 98^100。外围区域的体积（～出众者）= 100^100 –98^100。出众者所占比例 = (100^100 –98^100)/ 100^100。再次呼叫Wolfram Alpha，我们算出对于100个特征，86.74%的人是出众的。

对于200个特征，X(1),…X(200)，我们的模型给出：超立方体的体积（～总人口）= 100^200。内部超立方体的体积（～普通人）= 98^200。外围区域的体积（～出众者）= 100^200 – 98^200。出众者所占比例 = (100^200 – 98^200)/ 100^200。所以对于200个特征，98.24%的人是出众的.（再一次呼叫淡定的Wolfram Alpha。）

这就得到我们的结论。

当然，这只是一个模型。一如既往，这势必需要做出各种假设和简化。如果这个结果让你难以置信，你有两种选择。或者回头修改初始假设并生成另一个模型。或者接受这个结果并改变那个使你难以置信的成见。

 

在这种情况下，我们不得不接受这样的事实：高维的等边、直角、实心（！）方体的几乎所有材料都位于其外壳上。（实体）内部几乎是空的。

 

当我们考虑更高维的情况，数学有时候会导致意料之外的反直觉的——但是正确的——结论。并不是每个人都可以接受这个事实。

 

是的，在美国的选举季度，这是一个有寓意的故事。

 

微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文

新浪微博：http://weibo.com/duodaa

 

微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文

新浪微博：http://weibo.com/duodaa

 

 

美国有多个机构对大学进行排名，其中最有影响力的就是由《美国新闻和世界报导》在每年下半年公布排名，也就是常说的每年的USNEWS排名。日前，2017年USNEWS全球最佳大学排名已经公布。哈佛大学、麻省理工学院、斯坦福大学三所美国大学分列前三，而去年第三名的加州大学伯克利分校排在第四。
 
我们哆嗒数学网的小编最关心的还是数学学科的排名。去年中国学校在这个榜单的表现可以说是让人惊异——而今年——更进一步，可以说是惊艳！绝对的霸榜亚洲！
 
还是先说总体排名—前十名依然被英美法三个国家的大学完全占据。数学学科的前三名被美国大学包揽。第一名是普林斯顿大学，而麻省理工学院和斯坦福大学分列二、三名。另外四所美国大学，加州大学伯克利分校、纽约大学、加州大学洛杉矶分校、哈佛大学分别占据了第六、七、八、十的位置。法国的巴黎第六大学与英国的牛津大学并列第四。著名的剑桥大学位列第九。

 

 

再来说说中国高校在这个榜单的表现。在入围的200所高校中，中国高校占据33所。而全部亚洲高校总共才51所入围。另外，亚洲前十名里，有7所来自中国。说中国高校在USNEWS数学榜里霸榜亚洲，一点也不为过。

 

 

 

 

微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文

新浪微博：http://weibo.com/duodaa

 

 

原文作者：Ken Wessen，理论物理与人类生物学博士。

译文作者：333，哆嗒数学网翻译组成员，就读于中南大学数学专业。

校对：小米

​

 

 

微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文

新浪微博：http://weibo.com/duodaa

 

 

在这篇文章中，我打算用三个幻术让你惊奇不已。它们真的非常美妙。在这三个幻术中，正是无穷的概念让你的大脑一团乱麻。我想在意识到它是一个多么疯狂、令人激动的概念这一过程中，你会享受很多乐趣。

首先，我想让你思考一下由无穷多个物体组成的一个整体，或者说无穷集合，它的大小是什么。一个集合的大小简单来说就是它所包含的元素的个数。两个集合被认为是一样大的，如果至少存在一种方式能够将一个集合中的每个元素精确对应到另一个集合中的一个元素，并且每个集合里面都没有元素没被对应。

 

 

这个定义是有它的道理的。集合{1,2,3}与集合{A,B,C}是同样大的，因为我们可以这样作一个对应：1 ↔A，2 ↔B，和3 ↔C（当然，还有别的方式让它们一一对应起来，不过我们只需找到一个就行。）然而，当我们处理无穷集合的时候，事情就变得更有趣了。举个例子，考虑由所有正整数组成的集合{1,2,3,4,……}它和所有偶数组成的集合{2,4,6,8,……}是一样大的！这听起来很疯狂，扔掉第一个集合的奇数部分却仍然给我们留下了一个大小没变的集合，因为我们可以让它们的元素这样对应：1↔2，2↔4，3↔6，……第一个集合中的任意一个元素在第二个集合中都有唯一的元素与之对应，也就是它与它自身的两倍一一对应；同样，第二个集合中任一元素都可以和自身的一半建立对应。没有元素被漏掉，也没没被对应到的数；所以，奇怪的事情发生了，两个集合是一样大的。其它和正整数集大小相同的集合还有奇数集、由10的倍数组成的集合，甚至是由所有分数组成的集合。（这样的集合我们称之为可数无穷。）

现在我即将描述一个思想实验，用来展示基于这一事实的一些出人意料的结果。

打包乒乓球

让我介绍一下克拉克。他有一项超能力，能够让他完成一个数学家们口中的超级任务——在有限的时间内完成无限多的步骤。在这里，我们限定时间为一个小时，11:00开始，12:00结束。

有无穷多个乒乓球可供克拉克使用，并从1开始标号；还有一个袋子，克拉克可以用它来装乒乓球。

在11:00时，他拿起了第一批10个球，标号1，2，3，…10，并把它们放进了袋子里。接着，他从袋子里拿出了标号为10的球，其他的九个被留下。到现在为止，这些都小菜一碟，还没用到什么超能力。这时克拉克也应该休息一会，喝杯茶，因为接下来事情就不容易了。

等了30分钟，11:30，克拉克把标号11,12, …20的球放进了袋子里，又从中取走了标号为20的球。
 

又等了15分钟（11:45）他把标号21到30的球放进了袋子里，并取走了标号为30的球。

 

克拉克一直这么操作，总是先放进去10个球，又拿走第十个，但是每次等待的时间都变成了前一次的一半。

 

显然克拉克将要这样操作无数次才能把无穷多的乒乓球放进袋子里。所以，他能完成任务吗？

答案是肯定的。如果我们把克拉克在将下一批球放入袋子之前所等待的时间间隔加起来，就得到了和式（以小时为单位的分数形式）：

 

 

 

12:00时，当这个过程完成了，克拉克的袋子里装了多少球呢？

每一步，克拉克放入了9个球，这样操作了无穷多步，所以袋子里将会有无穷多个球。事实上，在所有正整数中，只有那些标号为10的倍数的球不在袋子里。这些真的都很显然。还没出现令人感到迷惑的事情——只需要集中一点点精神去仔细想一下这个无穷的过程。

 

但是，下面的事情就开始令人困惑了。

 

 

第一个幻术

假设，当克拉克在做这个实验的时候，他的朋友布鲁斯也在把无穷多的乒乓球放进一个袋子里。但是，他稍稍用了点不同的策略。

在11:00，布鲁斯拿起了第一批10个球，标号1, 2, 3, … 10，把它们放进了袋子里，但是他把标号为1的球从袋子里取走了。接着，在11:30，他把下一批10个球放了进去，标号为11, 12, … 20，又从袋子里取走了标号为2的球。15分钟后，在11:45，他把21到30号球放进了袋子，又从中取出了标号为3的球。一直这么操作，每一步放入10个球，但是又从袋子中取出标号最小的那个球。

布鲁斯的方法和克拉克的在本质上是否一样呢？嗯，每次他放进去10个球又取走1个，所以，看上去当然是一样的。

在12:00，当克拉克和布鲁斯比较他们各自袋子中乒乓球的个数时，他们会看到什么情景？

我们知道克拉克的袋子里含有无穷多个乒乓球，但是，令人难以置信的是，布鲁斯的袋子里一个球都没有！是的——0个。每个球都会被取出袋子。
 
 

思考一下：什么号码的球能留在袋中呢？这些球被标号为1，2，3…直到无穷，但是每个数字都一一对应这无穷多次放入-取出步骤中的一个，所以每个球都会被取出。举个例子，20号球在第20步时被取出，1529号球在第1529步时被取出，1327821号球在第1327821步时被取出。它们都消失了！

 

哇哦！太疯狂了。克拉克有无穷多个乒乓球，布鲁斯却一无所有。（作为一个有趣的转折，假想一下，这个实验不是用的乒乓球，而是用英镑的硬币，你被允许保留到了12:00时袋子里剩下的所有硬币。）

 

但是，当你想知道如果他们在时间结束前检查会发生些什么时，这甚至更为荒诞。

 

第二个幻术

假设布鲁斯和克拉克每一步都检查一下袋子而不是只在12:00检查那一次。他们会看到什么情景？

 

在12:00之前的每一次检查，他们都将会看到有相同数量的乒乓球。这是真的——每一次他们检查，乒乓球的数目都将严格相等。只有在精确的12:00那一刻，当无穷多的操作步骤被完成，才会出现差异——多么巨大的差异！那看起来就像是布鲁斯所有的球都在一瞬间消失无踪。

 

 

第三个幻术

 

理解并计算克拉克与布鲁斯的结果依赖于球的标号，所以现在让我们设想第三个超级英雄，戴安娜，也在那里做着相同的事情——每步放进去10个球，取出1个球。但是，戴安娜的乒乓球没有被标号并且是完完全全的不可区分。

 

在12:00时，戴安娜的袋子里将会有多少乒乓球呢？

 

抱歉——这时没有答案。这种情况下，我们已经从数学穿越到了哲学领域，所以这个问题留给你去思考、辩论。

 

讨论

也许你会觉得这些都太不现实，因为超级任务事实上并不可能？唔，在数学中这并不重要。我们对它们的思考、推理和研究都是可能的，数学中的许多东西都是如此。
 
 

 

举个例子，你相信三角形吗？它们是真实的吗？并不是。在现实世界中并没有如三角形的物体。它们只存在于我们的数学头脑中，就像无穷和超级任务以及很多其他的数学概念。我们看到的每一个“三角形”都只是一种近似——边并不完全是直的；角加起来也并不完全等于180度，等等。但这并不有损于作为一个数学实体来研究三角形和它们所有性质的重要性和必要性。

所以我们的乒乓球问题怎么跟无穷和无穷集合的数学产生联系呢？

在每种情景下，我们都在相加无穷多个球，并减去无穷多个球，但是∞-∞是无意义的：它可以有很多不同的答案，这已经为我们所证实。

乒乓球问题也阐明了两种方法之间的区别。把正整数集合和10的倍数集合分别排好并作一一对应可以表明它们是一样大的（这是布鲁斯的策略）：
          

                          
与之相对的是，从正整数集合中直接去掉所有10的倍数，留下一个无穷集合（这是克拉克的策略）：

 

                                                                                                                   

 

一些进一步的思考

1、 你可以尝试构造一个过程，通过在合适的时间，把克拉克的策略转变为布鲁斯的策略来使得袋子里最终留下的球数可以是任意一个指定的正整数。试试看，设计一个能够留下5个球的策略。

2、 戴安娜在参与实验的时候，球是不可区分的。考虑她的第k步放入/取出。
2.1  在这一步之后，一个随机的球还留在袋子里概率是多少？
2.2  在这一步和下一步之后，一个随机的球还留在袋子里概率又是多少？
2.3  你能用这些结果计算出在无限多步后一个随机的球留在袋子里的概率吗？
2.4  这个计算结果是否提供了一种方式，能够回答在无限多步后戴安娜的袋子里有多少个球？
2.5  在布鲁斯的情形中，他总是在取出球之前立刻放入10个球，那么最后一个球是怎么被取出以至于袋子里一个不剩？
   
3、 想象一下，在克拉克的袋子中有一个小妖精。当他试图取出10号球时，小妖精把数字0擦掉了，使得这个球变成了1号球；又给袋子里原本的1号球后面加了个数字0，使它变成了10号球。当克拉克取出20号球时，这个小妖精又这么做了——把20号球变成了2号，把原本的2号变成了20号。对于30、40号等等，它都如此进行。小妖精的重新标号是否意味着最终克拉克袋子里球的数量为0（就像布鲁斯一样）？
3.1 如果是，那么说清楚这是怎么回事？他取走的仍然是完全相同的那个球！
3.2 如果不是，那么最后袋子里剩下的那些球标号是什么？

4、 显然，超级任务是不可能实际做到的。那么你是否认为这些悖论表明了超级任务甚至在逻辑上都是不可能实现的？

 

 

微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文

新浪微博：http://weibo.com/duodaa

 

作者：N_a_O_H_ ， 哆嗒数学网群友， 常年活跃于数学贴吧。

 

微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文

新浪微博：http://weibo.com/duodaa

 

 

和朋友们聚餐吃饭，他们总会把最后验证账单的活交给我。我说我算不出来，还是按计算器吧。于是伴随着目瞪口呆，他们会惊诧地问我：“你不是数学系的吗？”

 

在诸多情况想，包括在研究中，这类体力活般的运算都交给了计算工具，比如说计算机。计算机，顾名思义，最初是人们发明出来代替人们进行计算工作的机器。随着编程语言被应用于计算机，人们可以精确定义给予计算机的指令，并且能以比人工计算快得多的速度得出结果，精确程度亦是令人信服。

人们利用计算机处理一个庞杂的计算任务时，依赖的是一种叫做循环结构的东西。这种结构把本身复杂的运算转化为一步一步的，每一步都依赖一个离散变量的小型计算，只需设定好想要的步数，就能令计算机按照这规定的步数进行一次次的机械的简单运算。就像织布机和流水线一样，这种简单机械的工作交给计算机是再适合不过的了，计算机运算的效率与准确程度都远高于人类。随着人们对数学的深入了解，指数函数，三角函数以及对数函数这些超越函数都可以通过这种循环结构计算了，而这些运算是初期的编程语言没有规定的。

 

泰勒公式是计算这些函数的一种方法，把上述函数转化为一个多项式，这些多项式每一项的系数也是有特定的规律的。这样，每一项的指数与系数都有规律可循，那么用循环结构执行就成为了可能。按照这种思路，就连定积分的计算也可以交给计算机了。

 

看上去很厉害，没错吧？

请仔细留意我上面的措辞。我说，计算机用泰勒公式去运算那一系列超越函数的函数值，这听起来似乎没有半点问题。然而泰勒公式是用一个多项式近似表示函数某点周围的性态，注意是近似！泰勒公式只是个有限项的多项式，只要你愿意你可以写出它的任意多项，但是它始终是有限项的。真正恒等于那些超越函数的是它们的泰勒级数，泰勒级数是一个无穷和。你用泰勒公式无论怎么精确，都只是泰勒级数的一个部分和，也就是其中有限项的和，其结果永远与精确值相差一些。

 

简单来说，得到上诉精确值或者近似值的方法，就是本文说的“数值计算”（这里打个引号，避免和真正专业的数值计算这个分支误会）。

计算机也可以计算定积分的数值，我们可以完全按照定积分定义相仿的思想来计算——取曲线下一列纵向的细长矩形面积之和来逼近曲线下的精确面积。这样的方法下，计算机无论如何努力，都只能把曲线下的面积化为有限个矩形之和，其结果自然与精确的结果有所偏差。当然，我们可以改进这些计算方法，比如把矩形改成梯形，或者利用根高级的理论简化步骤，但是我们得到的还是有限次计算得到的精确值或者近似值。

 

有人说，计算机进行了那么多次运算，其得出的结果的误差已经非常小了，以至于人们随时都能把它扔掉。不要着急，我完全没有要责难计算机计算能力的意思。我说了这么多，只是想说上述计算并没触及到数学的一个基础核心概念：无穷。

无穷这东西，其实并不像它们在实平面中那样离我们那么遥远，而是一直在我们身边。小学二年级引入了除法的概念，老师一再强调0永远不能作为除数。那时我想勤于思考的孩子都想过，那么0做除数会是什么后果呢，比如说1除以0？抱着好奇心他们把这个算式输进了计算器，得到的却是一个冷漠的Syntax Error，于是只好就此作罢。到了后来，随着知识的不断积累，学生们意识到了任何0之外的数除以0，得到的是无穷大，因为你无论有多少个0，它们的和就一定是0，所以结果只好是无穷大了。这种想法倒无可非议，只是流于想象，并不十分不严谨罢了。于是，“n/0”这类形式的无穷，大概就是我们最早能够接触到的了。

感谢数学家柯西和魏尔斯特拉斯，我们终于有了一种严谨的方式定义，证明和计算极限。那么我们回到上面的例子，我们还是来研究1/x在x=0处的极限。这次先让计算机来做。直接输入1/0会让电脑爆炸，所以我们只能通过一系列尽可能接近于1的数字来研究结果，1/0.1=10,1/0.01=100, 1/0.0001=10000, 1/0.00000001=100000000...千万不要以为这一系列结果告诉你很多东西，尤其是不能错误地就这几个结果，我们就臆断，x越接近于0，1/x越大，而这恰好是许多对数学不了解的人所犯的错误。数学中，对于有限的极限有这样一个性质：某处的极限存在（或者都趋于无穷），当且仅当每一个收敛到这点的数列，都收敛到一个相同值（或者都趋于无穷）。因此，为了用计算机证明这种极限，我们必须证明任意一个这样的数列都趋于正无穷，这将意味着我们必须验证无穷多个数列的结果，而且，就算我们能够验证无穷个序列的结果，那么对于这每个序列都有x趋于0时，y不断增大，注意我们能得出的只是不断增大这个事实，至于有多大呢？计算机暴力验证的办法，就行不通了。
 

来看另一方面，人们可以用极限的严格定义来证明，1/x在0处的值为无穷。容易验证对于任意给定的正整数N，存在0附近的某个点x，使得|1/x|>N。数学分析的知识告诉我们，1/x的绝对值可以比任何一个正整数都大，自然就是无穷大了。

 

从这里，我想引出这篇文章我真正想说的。我们数学系做数学的方式是用理性推理去证明数学问题的，这些数学命题很可能涉及无穷的概念。我们大多数人不会去纠结一个复杂的加减乘除运算式子，如何快速心算得到结果。比如，上面的命题“1/x在x=0处的极限为无穷”这一命题就是一个例子。暴力计算的思路很难验证一个涉及无穷的数学性命题，绝大多数情况下都只能验证有限个情况下命题的真伪性，而无法从本质上证明或证伪它。

 

下面我想再举另一个例子，这是我这周的C++课作业内容。作业要求编一个程序，来算采矿和淘金两种方法的收益，已知两种方法中，各有一定的概率获得一定数量的收入。要求设定一些随机变量，然后把程序跑1000000次，求平均数。这个作业的目的再明显不过了，无非是要验证数学实验的结果符合某个期望。作业中（具体的作业内容我不再叙述了）按照数学推理计算能得到数学期望的理论结果，采矿的期望收益为75美元，淘金为68美元。而用程序跑出来的结果，始终与这两个结果相差一些。诚然，如果你用程序模拟的结果最终成两个分别以75和68为中心的正态分布，或者能验证这个程序计算的次数越多（多于1000000次），结果越接近于75和68，那么自然是有说服力的。然而，尽管做出一个很大的样本，也不能从数学理论上认定，他们的数学期望就是75和68。如果要认定，两种情况都要求无限次的运算。而我们能通过有限次运算得出的，从某种意义上来讲是苍白无力的，看上去很接近75和68的结果根本不足以说明数学期望的存在性——无论他们怎么接近目标值。反过来说，倒是因为有了理论上数学期望的存在，多次运算后的结果一致地逼近某个数值，这样的一个结果才是可能的。我们熟知的投针实验和抛硬币实验都是一个道理。


这揭示了一个事实：在一些人认为很厉害的“数值计算”，在我们做数学的时候只是一个验证的工具，很多时候也许能给我们一些启发，但是大多时候一个数学理论突破的瓶颈跟计算机的这种计算没有半毛钱关系。甚至，我可以说严重一点，正如伟大哲学家康德也指出的，这些算式都是一个个经验性的命题，永远不会有真正的普遍性，从而没有指导意义。

 

这些“数值计算”够做到的，只是穷举和有限的运算，总而言之能做到的东西有限，不足以归纳证明带有任意性的命题，也就是本身蕴含着无穷的那些。实际上，计算机要做到真正的数学推理，需要换一种办法。这也是数学家们研究的一个领域，叫做机器证明。它的思路，已经不是“数值计算”去得到一些近似值，这个不是本文想讨论的范围。

 

 

在文章的最后，我想描述一下，有限在无限面前是多么渺小。

 

现在的计算机，如果要他完成一个需要2的500次方步骤才能完成计算，那简直是不可能完成的任务。但在，无穷面前，他可能只是一个很平常有限数，很多时候都可以忽略不计。比如，前面验证极限的时候，这个数字都出不了场呢！

 

说到底，这些“数值计算”可以覆盖的数学中的领域，标题上还高估了呢。所以，我是数学系的，但是是不会帮你们验证账单的。

 

 

微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文

新浪微博：http://weibo.com/duodaa

 

 

原文作者：Bruce Ferrington，数学普及作家。

译文作者：Humphrey Liu，哆嗒数学网翻译组成员，中学教师。

校对：Donkeycn

 

 

微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文

新浪微博：http://weibo.com/duodaa

 

 

致歉

 

今年三月，我出版了对一些杰出科学家的采访，咨询他们关于数学教育的经验和在他们的科学领域中是如何使用数学的。那时，我收到了传奇的计算机科学家、数学家高德纳教授的邮件回复，这封邮件却被我忽视而没有打开。

 

今天我收到高德纳一封礼貌的邮件，他想知道他之前的回复出了什么问题，为什么我没有告知他参加“科学中的数学”项目。当我检查我的收件箱时，发现那封邮件从三月以来一直在收件箱躺着（编者注：作者的这篇文章是同年的11月写的），而我没有打开和阅读它。

 

我感到深深地内疚，为自己的疏忽对高德纳教授致以公开的道歉。我也回复了他的邮件并致以真诚的歉意.

 

请阅读以下高德纳教授对我所问的十个问题而提供的慷慨回复.高德纳教授是斯坦福大学名誉退休教授，“算法分析之父”，若干计算机程序系统的创造者，字型设计系统Metafont的创造者，也是《计算机程序设计艺术》一书的作者——此书是计算机程序员的圣经。

 

以下为高德纳教授今年三月回复我的邮件的注记，他热心的评论让我感到更加惭愧错过打开他的邮件。

 

布鲁斯，你好

 

十个问题的回答如下！

 

对于学习来说，一个最重要的方面是如何问好的问题。你肯定把这一条学得很棒。

 

最美好的祝愿

 

高德纳

 

 

1、 描述你念书的时候数学课是怎样的？

 

我们这代人（在美国威斯康辛州）在二年级学乘法表，五年级学分数，九年级学代数，十年级学平面几何，十一年级学复杂算术，十二年级学立体几何。我提出的很多数学问题老师们都无法回答，所以我的大部分时间只能用于思考其他学科（英文，拉丁文，物理，化学，生物，音乐）的问题。但在我家，父亲有一台机械式加法乘法计算器，我很喜欢玩它。我花了数百小时用于画形如sqrt(x+a) – sqrt(x+b) (sqrt表示开方运算，其中a,b可以取不同的值)的函数图像，由于使用了不同颜色的铅笔，所以我可以将不同的图像画在同一张纸上。”）

 

 

2、 你在学校学的数学对你以后的生活有用吗？

 

绝对有用。我在数学课上学的东西没有一个不在反复使用的。例如，几何课不仅教我如何严格的证明，也为我创造字型设计系统Metafont语言提供了想法。很多字体是用这种语言设计的，这些字体正被全世界数以百万计的人使用。

 

3、 你心算需要有多优异才能在头脑中做计算？

 

我很欣慰我能记住乘法表直到12×12。不过我觉得记住更多（比如直到99×99）将浪费时间。仅仅当问题相当容易或者问题中含有符号而不仅仅是数字的时候，心算是非常重要的。当我做研究的时候，我通常开始时会使用很多草稿纸进行部分计算。而我边游泳边思考这个问题时，最终获得了灵感，然后通常就解决了能解决它。

 

4、 数学教导我们可以把两个事物放一起而创造一个新事物，这在你做的事情中重要吗？

 

复杂的结构是由简单的结构用简单的方式结合的。我认为计算机科学家能比数学家更好的明白这点，因为我们学会了如何在一台机器中表示多种数据。

5 、 数学是关于发现模式的。你在研究中需要寻找模式或者模式的反例吗？

 

是的，我觉得数学事实上是模式的科学。我日常处理的模式是一些事物之间的规律，而不是数字之间的规律。不过数值模式也非常重要：例如

1=1²,1+3=2²,1+3+5=3²,1+3+5+7=4² ,等等.

1³=1²,1³+2³=(1+2)², 1³+2³+3³=(1+2+3)²,等等.

 

 

6、 数学也教导我们平衡和相等，这种观念在你的研究中有用吗？

 

在前面提到的字型设计系统Metafont语言中，我们通过用某些关键的点应满足的方程所画的直线来表示字母A的形状。“左干从基线开始，距离边框左边沿半个单位，直到大写字高，左干的斜率等于右干斜率的相反数。”

[参考: 《计算机现代字体》，第369页。]                      

 

7、 数学帮助我们表示数量和数值测量，你工作中做这些吗？

 

实际上我描绘希腊字母π的程序，有两个地方使用了数字3.14159. [《计算机现代字体》，第159页。]

 

8、 估测足够精细吗或者你需要精确测量事物吗？

 

计算机科学家必须特别仔细，因为小的错误很容易被放大，并导致灾难性后果。
 

 

9、 你怎样使用统计来分析你的结果？

 

我工作很多都涉及比较不同的计算方法，以此确定哪一个最快。基本的统计，比如关于运行时间的最大值，平均值，中位数，以及方差在分析中是关键的。更大胆的说，在今天已知的大多数计算方法中，随机数和概率的概念是绝对本质性的因素。
 

 

10、 你还有其他的关于在你的工作中如何使用数学的领悟吗？

例如，当我刷牙时，我需要覆盖八个区域，分别为左和右，上和下，内和外。最有效的方式是沿着哈密顿路或者格雷码。

左上外侧

右上外侧

右上内侧

左上内侧

左下内侧

右下内侧

右下外侧

左下外侧

 

 

 

高德纳教授，非常感谢你回答这些问题，感谢你参与“科学中的数学”项目。你带给我很多思考，也希望能带给其他许多人思考，甚至在牙齿健康方面你也给了很好的建议。

再次为我在三月份项目早期没有包含你的观点而致歉。

 

 

 

微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文

新浪微博：http://weibo.com/duodaa

 

 

微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文

新浪微博：http://weibo.com/duodaa

 

 

从初中开始，我们就开始接触三角函数了。初中的时候，三角函数是在直角三角形中定义的。直角三角形中一个锐角的对边比上斜边就是这个角的正弦值，而余弦值被定义为这个角的邻边与斜边的比值。

 

 

初中的定义，使得我们对三角函数的研究停留在锐角的范围内。到了高中，我们利用单位圆和有向线段把三角函数的定义域扩大到了可以取到任意实数。于是，三角函数成了实数R到实数R的函数。

 

 

然而，如果你真较真儿的看看以上中学阶段的两种定义的话，你会发现以上两种定义方式都离不开“画图”，而看图说话的方式依赖人的感觉——视觉，这不是一种数学意义上的严谨方式。再深入一点，单位圆和有向线段定义三角函数的方式，需要把角的大小对应成为实数，而对应实数的方式，要么用到某个扇形的面积，要么会用到圆上某段弧的弧长。然而，你在圆上截取的这部分扇形的面积，或者那段弧的弧长分别存在的理由是什么呢？奥，你会说我画出来了，看吧，它就是占了一块地方，或者就是一截长度——我相信是对的，但是这样的理由依然是感觉的，而非数学逻辑的。

如果，按数学严谨的逻辑应该怎么做呢。我们可以完全依照公理与逻辑从自然数理论（可以用ZFC或者皮亚诺公理导出自然数的相关理论），发展出有理数理论，再而发展处实数理论。理由实数的完备性的公理，发展处极限理论、微积分理论，再而级数和微分方程理论。这些基础，都可以只依赖于公理体系和形式逻辑，而不依赖与感觉。于是本文就用这些理论来定义三角函数，已经推倒三角函数的性质。——本文将用无穷级数定义三角函数。利用无穷级数或微分方程也是到目前为止，严谨的定义三角函数的最佳方案。

定义三角函数的核心也就是定义正弦和余弦函数，下面我们会围绕这个来展开讨论。

我们用级数来定义下面两个函数：

 

 

我们后面证明的公式，很多可以利用级数之间的四则运算直接得出(比如2sinx cosx = sin(2x)之类)，但是我们哆嗒君并不打算这样做，下面所有的关键推导，我们都尽量避开一些艰深的级数间运算的技巧，虽然那很直接（比如证明存在使得sinx小于0的x的时候，可以直接估计计算sin5,sin6之类），但是，对一些普通人来讲，那过于麻烦了。

1、    π的定义

上面两个级数对任意实数x都是收敛的。而且很容易看出sin0 = 0， cos0 = 1 。

另外我们也很容易得到上面两个定义后的函数的奇偶性，即是说：

 

 

根据无穷级数的相关理论上面的两个级数都是连续，可微，且求导导数的时候还可以使用逐项求导的方法。

于是我们得到

 

 

于是有，

 

 

说明sin² x + cos² x 是常数，代入x = 0，得到

 

 

利用上面的式子，我们还能得到关于两个函数的上下界的不等式。

 

 

注意到sin x 连续可导，导函数在零点为cos0 = 1 > 0,说明sinx 在0 点的某个右邻域内单调递增，从而在某个区间(0,δ)上，sin x > 0。(*)

 

我们估计一下来说明sinx存在大于零的零点。这只需要说明sinx有取得负值的点。显然，sinx，cosx在任何区间上都不恒为常数，于是我们假设sinx > 0恒成立，这时cosx是单调递减的，用下面两部分文字来推出矛盾。

 

若cos x 非负恒成立，则有sinx单调递增，于是由单调有界原理，可设

 

 

则由拉格朗日中值定理，有下面的矛盾：

 

 

若存在y使得cos y小于零，那么当x≥y时，cos x < 0，说明在这个区间上sin x单调递减。

 

于是由单调有界原理，可设

 

 

则由拉格朗日中值定理，有下面的矛盾：

 

 

于是，存在y，使得siny < 0，也就是说存在x > 0，使得sinx = 0。

 

于是我们把下面的实数定义为π。

 

 

因为sinx的连续性和(*)的结论，上面的下确界inf符号其实可以换成最小值min，即有π > 0 ，sinπ = 0 。

 

2、 和角公式和诱导公式

 

这一部分的内容需要用到常微分方程的相关理论。

 

注意到，sinx与cosx 都满足下面这个二阶常系数线性方程：

 

 

因为sinx和cosx是线性无关的。于是上面方程的解一定有形式：

 

 

而对应任意实数y，sin(x+y)也满足上述方程。所以

 

 

代入x = 0，x = -y 得到

 

 

同理可得，

 

 

于是我们得到了和角公式。

 

令x = y = π/2 , 得到

 

 

注意到由π的定义可得sin(π/2) > 0，可以得到 cos(π/2) = 0, 从而利用sin²x+cos²x=1这个式子得到sin(π/2)=1。再利用一下cos x 在[0, π]的单调性（由π的定义这个区间上cosx 的导数-sinx 非正），得cosπ=-1。

 

于是反复使用以上公式，我们得到诱导公式，

 

 

于是我们知道2π是sinx 和 cos x 的一个正周期，实际上它还是最小的正周期。比如用sinx来说，2π不是最小的正周期，那么存在正数T < 2π还是sinx的正周期，下面三种情况都会得到矛盾。

 

  若T < π ， 则 0 = sin0 = sin( 0 + T ) = sinT ≠ 0 。

  若T = π ， 则 1 = sin(π/2) = sin(π/2 + π) =- sin(π/2) = -1  。

  若π < T < 2π ， 则 0 < T-π< π ， 有 0 = sin 0 = sin( 0 + T ) = sinT = -sin(T-π) ≠ 0 。

 

于是，正弦和余弦函数关于周期的性质我们也得到了。

 

反复利用和角公式，我们得到正弦和余弦二倍角公式是三倍角公式。

 

 

利用这些公式，我们得到常用的一些特殊锐角的值，

 

 

 

3、 反函数

 

我们已经知道，-sinx 在[0,π]内是非正的，且只有孤立的x = 0，π两个点上取得零值。这说明,cosx 在[0,π]上是式单调递减的，于是在这个区间上有反函数，记为arccos x。

 

而sin x = cos(π/2 - x) ，利用复合函数的性质，得到sin x 在[-π/2, π/2]上单调递增。于是sin x 在这个区间上有反函数，记为arcsin x 。

 

特别的，我们有arcsin 1 = π/2 ， arcsin (1/2) = π/6， arcsin 0 = 0。

 

利用反函数的求导法则,对y=arcsin x求导，得到，

 

 

同理有

 

 

 

好了，我们已经把正弦和余弦函数的中学中常用的性质推了个遍，那他和圆有什么关系呢？

 

 

 

4、 圆的周长和面积公式

 

我们知道，圆的周长和面积都是由解析式x²+y²=r²(r > 0)，所围成图形决定的。而对于这样图形的面积和曲线长，我们利用积分（依赖于极限）有严谨的定义。

 

对于面积，由于对称性，我们计算下面这个定积分的4倍。

 

 

而对于后面的积分，令其为I，我们有

 

 

得到I = πr²/4 , 那么它的4倍就是半径为r的圆的面积,πr²。

 

对于连续可导的函数y = f(x) ，在区间(a,b)上的那一断曲线长为： 

 

 

于是由于对称性，圆的周长就是下面这个定积分积分的4倍。

 

 

于是4倍就得到半径为r的圆周长2πr。

 

我们通过上面的积分计算，建立起了圆的两个重要几何性质与之前定义的π的联系。最后我们要看看，π的值到底是多少。

 

 

 

5、 π的值是多少

  微积分中，我们知道，下面的公式（|x| < 1，规定(-1)!!= 0!! = 1）：

 

 

得到：

 

 

两边积分有，

 

 

代入x=1/2 有

 

 

这个级数的收敛速度还不错，要计算到3.14…..的精度只需要计算4项，计算到3.1415926......的精度只需要10项，耐心一些用手算都可以出结果。它比一般高数书给出的用arctanx的展开式计算π/4的速度快了不少，而后者，就算计算到500项也得不到3.14......的近似值。

 

 

学数学一定追求严谨到极致？

 

有句话说得好，数学的严谨就像衣服，太紧了不行，太松了不好。如果用这种最严谨（目前）的方式来作为起点学习三角函数，这种丧失全部直观的方式其实并不符合人们认识新事物的规律。另外，由于理解这种方式，需要对实数理论、微积分相当熟悉，而后者要到大学才开始接触，会拖后三角函数的学习进程。毕竟大部分人使用三角函数，都是使用其函数性质而非它的逻辑底层，完全没必要把这部分知识放在那么后面。

但是，如果我们追求一个理论的逻辑上的完美，在有一定数学功底之后，来回味一下从实数的基本理论来建立三角函数（或者其他初等函数）的过程，借此品尝一下数学的“极致严谨”小甜点也是一件很有趣的事情。

 

 

微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文

新浪微博：http://weibo.com/duodaa

 

原文作者：Alex Bellos，巴西数学科普作家。

译文作者：xyz，哆嗒数学网翻译组成员，就读于华东师范大学

校对：小米

 

 

赌博有其罪恶之处，却有助于塑造现代社会。本文中，数学家亚当•库哈尔斯基讲解了赌博和纸牌游戏启发科学领域中许多原始想法的方式。

 

微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文

新浪微博：http://weibo.com/duodaa

 

 

 

1.掷骰子游戏和新科学的诞生

十六世纪时，运气是无法被量化的。如果有人在一局摇骰子游戏中摇出两次6点，人们认为这是运气使然。吉罗拉莫•卡尔达诺，一个一生好赌的意大利籍物理学家，却并不这么想。他决定用数学方法处理赌博游戏，并写了赌徒手册，里面描述了如何驾驭概率事件的“样本空间”。例如，两个骰子有36种放置方式，但只有一种是两个6点。

这就是概率论的起源。这意味着我们可以量化一件事的可能性，并精确算出我们有多幸运——或者多不幸。多亏他的新方法，卡尔达诺在赌博中挣到了很大一笔钱，同时，数学也有了一个新的研究领域。

 

2.点数分配问题

假设你和一位朋友玩掷硬币游戏，并且第一个赢六次的人得到£100。如果游戏在你5-3领先时结束，你们该怎么分这一笔钱？1654年，法国贵族安托瓦尼•贡博就上述的“点数分配问题”向数学家费马和帕斯卡寻求帮助。

为了处理这个问题，费马和帕斯卡发明了名为“期望”的概念。这个新概念指的是：如果游戏被不断重复进行，每一方平均获胜次数的比例。现如今，这个概念是经济和金融的重要部分：通过计算一项投资的期望，我们可以算出该投资对每一派的价值是多少。

在掷硬币游戏中，你的朋友（3-5落后）需要连续掷对三次才能获胜。这件事发生的机会是1/8，而你平均在8局游戏中会赢得其余7次。因此，这笔钱应该以7：1的比率分配，也就是£87.50对£12.50。

 

 

 

3.轮盘赌和统计学

19世纪90年代，摩纳哥报会经常刊登蒙特卡罗赌场的轮盘旋转结果。在当时，这正是卡尔•皮尔逊想要的。他对随机事件极感兴趣，并需要数据去证明他的方法。不幸的是，轮盘不像他期待的那样随机。“就算蒙特卡罗轮盘从很远很远的地质时期就开始转动，”皮尔逊在研究数据后说道，“我们都不指望报纸上这两周的轮盘结果会出现——哪怕一次！”

皮尔逊的方法，经过轮盘分析的打磨，已成为科学的重要组成部分。从药物试验到欧洲核子研究所的实验，实验员计算完全靠运气获取结果的几率，并依此检验理论。这使他们能够确定是否有足够的证据支持他们的假设，或者这些结果是否只是巧合。至于皮尔逊持续关注的轮盘数据，下述解释更接近真相——懒惰的摩纳哥报记者并没有记录轮盘结果，而是捏造了数据。

 

 

4.圣彼得堡彩票问题

假设我们进行如下游戏，我反复掷硬币，直到正面第一次出现。如果正面在第一次掷就出现了，我给你£2。如果正面在第二次掷时出现，我给你£4。如果是第三次才出现，我给你£8，依此类推，每多一次，金额翻倍。那么，你愿意付我多少钱来玩这个游戏？
    
由于其期望值（也就是当这个游戏被进行很多次后，其平均支出）极其巨大，这个名为圣彼得堡彩票问题的游戏使18世纪的数学家感到困惑。然而，很少有人愿意花一笔钱钱来玩这个游戏。1738年，数学家丹尼尔•伯努利通过引入“效用”的概念解释了这个困惑。一个人的钱越少，他就越不愿意在赌博中冒大风险赚大钱。效用现在是经济学领域的核心概念，实际上也支撑着整个保险行业。我们大多数人宁愿进行小的定期投资以规避潜在的巨大风险，即使我们总体上会收获更多。

 

5.轮盘赌和混沌理论

1908年，数学家庞加莱出版了《科学与方法》，他在该书中思考我们做出预测的能力。他指出像轮盘赌这种游戏的随机性在于球的初始速度的差异——这种速度很难准确测量——并对球的落点有很大影响。20世纪下半叶，这种“对初始条件敏感的依赖性”成为“混沌理论”的基础概念之一。其目的是研究对于物理与生物系统可预测性的极限。

当混沌理论成为一个科学领域时，其与轮盘赌的联系依然存在。20世纪70年代，混沌理论的开拓者的其中一部分是像多因•法默和罗伯特•肖的物理学家——他们把电脑偷偷地带到赌场中，以测算轮盘赌中球的速度——并用这些数据成功预测了结果。

 

 

6.纸牌游戏和模拟的力量

计算机在概率学中有重要地位。20世纪40年代，计算机有了重大发展，这要归功于一位名为斯坦尼斯拉夫•乌拉姆的数学家。与许多同行不同，他不喜欢进行冗长的计算。他曾经打坎菲尔德牌戏——一种源于赌场的单人纸牌游戏——并思考以怎样一种方式才能赢得游戏。这位数学家意识到与其尝试并计算所有可能性，还不如多进行几次游戏并观察结果。

1947年，乌拉姆和他的同事约翰•冯•诺依曼应用了一项新技术用以研究位于新墨西哥州的洛斯阿拉莫斯国家实验室中的核连锁反应，并给它起了代号“蒙特卡罗方法”。通过使用计算机重复模拟，他们可以解决那些对于传统数学来说过于复杂的问题。自那时起，蒙特卡罗方法成为了从计算机图形到疾病疫情分析等众多行业的重要组成部分。

 

7.扑克牌和博弈论

约翰•冯•诺依曼在很多事情有辉煌成就，却并不擅长扑克牌游戏。为了研究什么样的策略更有效，他决定用数学方法分析游戏。尽管如何处理卡牌是一个概率问题，单纯解决这些问题并不足以获胜：他还需要预测他的对手的行动。

冯•诺依曼对于扑克牌和百家乐这样的游戏的分析引导他进入了“博弈论”的领域，也就是研究不同玩家的策略和决策的数学领域。约翰•纳什在冯•诺依曼的基础上进行研究，他的故事被翻拍成了电影《美丽心灵》。自那时起，博弈论逐步进入经济学，人工智能，甚至是进化生物学。也许由赌博引发的想法渗透进了如此多的领域并不会让人过于惊讶。正如冯•诺依曼所言，“真实生活中充满了虚张生势”。

 

 

微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文

新浪微博：http://weibo.com/duodaa

微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文

新浪微博：http://weibo.com/duodaa

 

原文作者：John Baez

译文作者：Donkeycn，哆嗒数学网翻译组成员，华东师范大学。

 

 

微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文

新浪微博：http://weibo.com/duodaa

 

 

一个三次曲面是一个由3次多项式方程所定义的曲面。一个结点型曲面是一个仅有的奇点都是普通二重点的曲面：也就是说，它的奇点看起来就像是3维空间中按下面方程所定义的锥面的锥顶。

 

 

x² + y² = z²

 

 

凯莱三次结点型曲面（参见上面由 Abdelaziz Nait Merzouk 给出的图），是拥有最多（即4个）可能的普通二重点的三次曲面。事实上，每一个拥有4个普通二重点的三次曲面都与它是同构的。

 

 

 

 

凯莱三次结点型曲面可由如下方程定义：

 

wxy + wxz + wyz + xyz = 0

 

 

该方程定义了一个复维数为2的C⁴的子集S。需要注意的是，如果(w , x , y , z)∈C⁴是该方程的解，那么它的任何倍数(cw , cx , cy , cz)也是。因此我们可以射影化S，将任何一个解与它的任何倍数视为是相同的。于是我们得到了复射影空间CP³中的代数簇X。该簇具有复维数2，所以它被称为一个复曲面。为了获得一个普通的实2维曲面，我们将它与CP³中的一个RP³的拷贝作交集。

 

 

现在让我们着眼于RP³，相应地我们将得到很多普通3维空间R³的拷贝。上面的图片显示了凯莱三次结点型曲面在其中一个拷贝中的部分图像。

 

 

凯莱三次结点型曲面的简单二重点出现在w，x，y，z中有三个坐标为零的地方。超平面w + x+ y + z = 1决定了CP³中的一个C³ 的拷贝；并且如果把所有四个坐标都限制为实数时，将给出一个R³ 的拷贝，同时这些二重点恰好构成一个正四面体的四个顶点。此外，凯莱三次结点型曲面的对称群是S₄，即正四面体的对称群。

 

谜题1. 凯莱三次结点型曲面上有9条直线。其中6条包含了上述四面体的棱。那么另外3条呢？

 

下文讨论了凯莱三次结点型曲面的一些有趣性质：

 

·Bruce Hunt, Nice modular varieties, Experimental Mathematics 9 (2000), 613–622.

 

特别地，他解释了它是如何作为一个球的商的紧化以及某特定的阿贝尔4-流形的模空间。

 

 

谜题2. 证明：通过变量代换，凯莱三次结点型曲面也可以由如下方程定义。

 

 

w³ + x³ + y³ + z³ = (w+x+y+z)³

 

 

 

微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文

新浪微博：http://weibo.com/duodaa