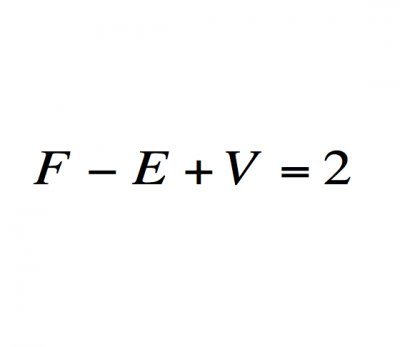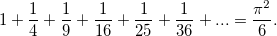微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文

新浪微博：http://weibo.com/duodaa

写在正文之前

我关注哆嗒数学网时间虽然不长，但是作为一名数学爱好者，我仿佛找到了一个理想的彼岸。我曾在数学吧、33IQ等多个平台里面以提问和故事的形式分享我的“愚见”，一些零星的反响，带给了我不断探索的勇气与激情。偶然的机缘，我结识了哆嗒数学网，里面丰富多彩的数学故事、知识，以及经久不衰的书籍，让我叹为观止！本次我所参与的写作征集活动，也让我找到了一个能“畅所欲言”的舞台。祝愿哆嗒数学网能够充分利用互联网的优势，让数学那道神圣的光芒，照耀到每个默默为数学探究努力付诸行动的人。

最后我对搭建哆嗒数学网，以及背后那些为这个平台的正常运作而默默付出的人表示由衷的感谢！

作者是一名能为自己的目标而不懈追求的人，在他年轻的时候就被那包罗万象的波尔兹曼方程所吸引，与大多数数学家一样，围绕在他们周围的始终是堆积数米高的草稿子，一台笔记本电脑，一支笔，以及在自己所热衷的难题与生活面前数以万计的选择。他们是一群敢于在黑暗中前行的人，穷尽自己的智慧与胆识力求在黑暗中寻找出一条通向光明的道路，在这之前，或许他们也并不知道自己在哪儿，距离成功还有多远，唯一支撑他们继续前行的永远是那个最单纯的信念以及永不磨灭的好奇心，有人把定理和数学家的关系描述成：定理是在某个正确的历史节点上选择了一个正确的人来证实了自己的存在，而这个唯一接近真理的人在此之前却又是终日与孤独为伴，相逢的知己也就自然而然的成为了他生命中最难忘的人。对于隐藏在问题背后的本质，数学家们有着极其敏锐的嗅觉，即便已超越平凡的认知，可对于数学家来说，他们并不会停留于此，一颗追求完美的心，会时刻让他们陷入更深层次的世界里面。

本文的作者塞德里克·维拉尼，一个多才多艺且充满传奇色彩的数学家，与其他数学家一样，为了自己心中拟定的那个奋斗目标能够变成现实，他奔走于各所大学开展不同程度的学术讲座，从普林斯顿研究所再到庞加莱研究所，其间也不断的进行着各种深度的学术交流活动，结识了一些志同道合的朋友并且畅谈一番；与此同时，他也与普通人一样，有一个幸福美满的家庭，为了扮演好一个父亲的角色，他不忘准时去接送孩子上学，逗他们开心，陪伴他们健康成长。与常人不同的是，他目标非常明确，并且能为自己的目标而付出十倍于常人的努力。

朗道阻尼——粒子和波相互作用使波的振幅减小的现象。也许正如达尔文所述：“数学家就像是在黑暗中努力寻找黑猫的那一类人。”朗道阻尼就如同那只黑暗中的黑猫，因为从一开始，它就单单只是个猜想（尚未有被公认的数学表达式）。但是由于这个猜想所描述的等离子体的自发稳定性规律，让深处波尔兹曼方程正则性问题困惑的作者在冥冥之中嗅到了其中的关系。万物归宗，大到恒星自发组成具有稳定外形星系的神奇能力，小到等离子体的自发稳定性规律。二者虽然来自不同的研究领域，可在表述上却又不乏相似之处，或许能从相似的现象中可以提炼出相似的研究方法呢？通过把离散的恒星群体的运动近似的看作为连续的流体来进行研究，再对误差进行控制分析，从中导出与“最优运输”的关系，这一切的关联给作者带来了启发。在对以上部分的阅读中让我深刻的感受到了数学的神秘性，方向不同但思维方式却可以引起共鸣，再通过彼此之间的相互交融最后产生灵感。另外让我为之一颤的是文中所提到的 KAM 理论，它所描述的某些局部扰动并不能改变全局结构的特性，引起了我的共鸣，仅依靠自身的系统规律来实现局部无序到全局有序的转化，这种局部与整体不相一致的模式让我联想到了 IMO 中的一些情形：局部最优并不意味着全局最优。

文中不乏有晦涩的专业术语，细细品味之后，抛开不明觉厉的感觉，呈现在我眼前的那一道又一道思维亮点，让我叹为观止。在高层次的数学领域中，更趋向与把研究对象分解，从系统性的角度来研究其具有的性质，通过精确的定义、严密的推导、巧妙的构造，实现思维模式到解法的转化。天书般的数学符号像一个个彼此相连的音符，他们紧密而又美妙的组合，成为了响彻整个宇宙的天籁之音，高度概括性、抽象性、层次性的特点让它失去了初等数学那样的亲和力，里面所涉及的符号就像一个个机构一样庞大而又复杂，对深层次规律的探索时刻让我感受到一种“道可道，非常道”的压力。不过，万变不离其中，只要我们目标
明确，问题表述清晰形象，就不至于感到迷茫，数学背负着解释万物的使命，作为一门语言，我们用它来描述其他语言因为其自身的局限性而不能很好描述的现象，其操作过程往往是先把对象抽象出来在赋予其形象化的特征，这时问题很可能就转化为了一个能被解决的问题。

灵感引领我们取得突破的第一推动力，在研究过程中作者也曾多次陷入不同程度的困惑之中，忘我工作的状态之后，迎来的并不全是疲惫与绝望，上帝最喜欢在这个时候抛洒灵感的火花，指引着他走出困惑，爱迪生曾说过：“成功是 99%的努力加上 1%的灵感”。而我更情愿不这句话改为“成功是用 99%的努力去换取那 1%的灵感，再用那 1%的灵感去指引随后 99%努力的方向，直到最后取得成功”。诚然，努力也不一定会成功，必要的时候需要跳出死胡同，当正向进展受阻，不妨考虑从逆向进展，如本文所做：把某个部分可能出现的解所具有的特征提取出来进行分析，对特征解的分析能加深对整个系统的认识，有助于走出困境。当然以上方法极具特殊性，普遍来讲，解决一个数学难题最常见的两种情况是：1.突破性发现。这种情况又可细分为两种：1.1 已有的数学工具相互组合形成一个能带来突破性发现的数学工具，例如：微分几何就是微积分学与几何学交融后所形成的一个新领域，复变函数就是复数与函数交融后所形成的一个新领域。依靠这种突破性发现来攻克数学难题的数学家是极具眼光的一类，这让我联想到了解决庞加莱猜想的俄罗斯数学家佩雷尔曼，其核心工具“里奇流方程”，一个描述空间图形形状，即使在连续变化过程中出现干扰，但也最终偏向均匀分布变化而不改变拓扑结构的规律的方程。虽然佩雷尔曼不是发现里奇流方程的第一人，但他却将非线性几何偏微分方程用于拓扑学研究，并取得成功的人，这归功于他独特的眼光。1.2 敢于打破已有的数学工具，开创出一套崭新的数学工具用于问题的研究，例如：日本数学家望月新一，据说他就开创了一套前所未有的数学工具——宇宙际 TR 理论，用于解决困扰数学界已久的数论难题——ABC 猜想，可是由于目前还没有建立起一个好的标准来对此进行审核，所以研究的结果也就被搁置一旁，无人问津。这种情况很少，毕竟当前数学研究模式依然是把研究成果建立在彼此合作之上的。本文作者力图构造一个能便于自己研究的范数，构造是一项极具挑战性的工作，在各种条件所限制的前提下，为自己争取尽可能大的可突破空间，可事情往往不是单向发展的，构造出的模型在用于研究的过程中随时都会遇到新的问题，这是我们会在局部与全局之间做出选择，运气好的话，通过相关的技术能够完成在局部范围内的修复，研究的以继续，诚然，无法得到修复的局部错误波及到全局，对其产生显著影响的时候，那么就只能打道回府，另辟蹊径，“说到底，你所做的这些事，随便一个笨蛋都能做到，你应该去寻找一个更重大的问题，让人生更有意义”。

数学是一门极具艺术性的学科，一串看似简单静止的字符表达，却是一个复杂系统的缩影。是真理的传递形式的体现，是大量信息的浓缩体，艺术性的表达式成就了包罗万象的数学定理。数学是一门极具神秘性的学科，文中谈到格罗莫夫对纳什所提出的“非光滑嵌入定理”的评价是“这不应该存在，但确实存在”。数学是理论性很强的学科之一，它具有前瞻性，它推动世界的发展，但又超越现实的脚步，如今的数学已发展到及其抽象的阶段，即使是跨分支的交流也变得吃力，也许某些研究对象并不能在现实中找到实际意义，但是却能推动数学理论的发展，例如虚数单位 i，找不到实际意义，但却成为了复变函数的基础，而复变
函数的发展却有着实际的意义。这种虚实之间的转换更是给数学披上了神秘的面纱，殊不知还有多少这样“默默无闻”的东西等待去发掘。数学是一门极具吸引性的学科，一个都能看懂，都有话可说的命题，却是一声跨世纪的问候，费马大定理、哥德巴赫猜想，叙拉古猜想......它们是时代的句号；先辈们的省略号；智者的问号；胜利者的感叹号。数学是一门极争议的学科，1976 年，哈肯通过计算机对一千种构形加以检验，以此证明了四色猜想。关于这种依靠计算机来完成理论性的证明的行为，是否有悖于数学证明的初衷，成为一个备受争议的话题，计算机作为时代发展的产物，理应肩负起时代的使命，与人类合作发展，它是人
类智慧的体现形式，用它来辅助进行证明证明过程中所遇到的极其复杂的运算，是不影响人类在研究数学过程中所形成的思维模式，相反，计算机的合理使用会有助于提高我们对于运算本质的认识。数学是一门及其严谨的学科，尽管作者已经证明了在大尺度时间前提下的朗道阻尼，但是依然遭到不少人的质疑，于是他又带着“能否在无限时间条件下成立？”这个疑问，直到成功。一丁点的瑕疵，却使价值含量大打折扣，完美的定理周围总是围绕着一群苛刻的人。

“人应该把自己放在逆境中，才能成长”，致力于现实之中，却置身于希望之上。

微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文

新浪微博：http://weibo.com/duodaa

作者： e^iπ+1=0，就读于上海科技大学生命科学学院。

投稿可发至邮箱1178853280@qq.com，详情参见征稿说明。

微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文

新浪微博：http://weibo.com/duodaa

中国古代对于世界的认识是循环闭合的体系，千变万化的现象背后存在着某种联系，它们相互依赖；而西方对于世界的认识是基于直链单向的因果，从一般的抽象化的概念与产生的衍生来解释特殊的现象。这两种思考导致了根本性的区别，那就是中国古代注重对于事物的理解，利用一个现象去解释另一个现象，发掘内在关联；而西方更注重于逻辑，建立一般理论将所有的现象统一于理论之下。进而我们能理解，为何西方可以诞生近代公理化，高度抽象化的数学体系，而中国数学则不成体系，以原始形态呈现在数学家面前。

基于以上理解，我们不难理解，虽然中西方数学的起源非常类似，都是基于对于生活实践中遇到的问题进行归纳和理性的处理，然而中国数学的发展一直在延续前人的研究传统，即以直观现象或实例为基础，并加以运用。

需要指出的是，西方近现代数学发展（从16世纪开始），与西方现代科学发展的传统，并非是直接继承从古希腊时期开始，由几何原本奠定下的公理化研究方法。事实上当我们考察无论是近代数学还是物理学的发展之初，都基于对经验事实的依赖和大胆的猜测与想象。从这一点上，中西方差异在于，西方率先使用一般的，抽象的方式来解释特殊问题，坚信世界所有的现象可以被统一在数中。不仅如此，他们善于从复杂的现象中归纳出“优美的性质”，并且坚信优美，简单的理论是世界的终极解释。所以16世纪初，数学与科学的蓬勃发展中，无不透露出对于这种朴素哲学观的贯彻。比如开普勒，早期的天文学，数学的探索者，在其重要著作《世界的和谐》中指出，将天文学与音乐完美结合在一起的可能性，并且被看作是世界的和谐。而这种朴素认识论正是西方近现代科学的开端。

第二个重要问题是数学体系的建立和推演。必须承认的一点是，在体系的建立和推演上，中西方数学早早地分道扬镳。以《九章算术》为例，从内容上，中国古代数学问题的核心在于对实际问题的解释和再利用，故而卷分类以“方田”，“粟米”，“衰分”“少广”，“商功”等等实际生活场景进行分类。但是从数学内容上，九章算术不仅处理了大量复杂问题，而且包含了重要的哲学思想（如极限，分割，组合等）。最为流传的例子即“祖暅原理”，即判断两个物体的体积相同，可用“幂势既同，则积不容异” 这一原则进行判断，并且利用这个原理求出“牟合方盖”体积（所谓“牟合方盖”是指相同的两个圆柱正交围出的立体形）而这个立体形的体积求解是无法用初等数学解决，严格来说应使用微积分才能完全解决。而从其论述中，我们能看到朴素的积分思想，也展现了古代数学家杰出的数学直觉。同时，在研究的领域上有极大的弹性，从初等代数，初等数论到初等几何学（基于现代数学的观点）中的各个问题都有涉猎，并且给出了认识解决问题的重要思考。如卷八方程篇的开篇问题，即利用方程组思想解决问题，而以西方数学观点来看，所利用的正是高斯消元法。 再如广为乐道的中国剩余定理，以及勾股定理，涉及到了初等数学中大量重要核心命题。但是，从推导上，我们所给出的叙述性解释为主，而并非推导和计算。事实上，在《九章算术》中，只有遇到实际例子和少数公式上会进行计算，而原理性内容作为理解出现。 在这种情况下，数学的发展仅仅依靠极少数数学家不加证明的洞察给出进步，对于体系的发展本身是致命的。

而在西方，数学的发展在初期也是大胆而富有想象力的，不过他们并没有停留于理解，而是用相对细致的逻辑链组织成数学语言表达出来。数学的活力最早是在艺术家的手上复活，无论是绘画（透视画法对射影几何的影响），音乐理论发展，激发了人们的思维。16,17世纪数学家的工作时常是不严谨，甚至也没有任何数学公理基础的保证，如欧拉关于很多无穷级数的处理，都是基于一些朴素的认识，从形式上获得灵感便不加证明的使用。这个阶段的数学，思想上的推动力其实与中国古代数学家一样，依赖于数学家的直觉进行研究。但是，之所以西方数学在经历相似时期之后有爆炸性发展，原因有二。其一，使用抽象符号对数学进行描述，使得数学从实际问题中解放出来，可以自由地组合，用简单方式刻画复杂事物，发挥想象力，不再受制于具象。其二，相对中国古代数学，西方数学家更重视逻辑链的建立，所以从因到果的过程更细致，为之后的研究打下坚实铺垫。而我们津津乐道的数学公理化与抽象化的工作都不是在早期完成，而是在18世纪开始被越来越多数学家重视。分析学的诞生事实上就是数学家对于精细逻辑链的探索，为微积分打下坚实理论基础，同时揭示了大量显然命题正确性的由来，使得人们对微积分体系认识更为深刻。与此同时物理学的蓬勃发展推动了大量计算技术的发展，将微积分应用至实际研究中去变成了一种共识。进入19世纪后，一方面微积分席卷了几乎原来所有的初等数学分支，另一方面近代代数学的发展提供了抽象工具，如群论，用以解释方程解而诞生的理论，所以接下来发展的数学分支变成了群论，复变函数论，几何学也焕发新的光芒。进入20世纪后，无论是公理化还是抽象化的工作都达到了顶峰，数学家意识到各个数学分支间是有紧密联系的，拓扑学，集合论，抽象代数的发展将零碎的研究和数学分支网罗在相互联系的，统一的架构中，真正成为一套体系。 从这一点上，中国古代数学传统是不可能演化出这样的体系的，其原因不仅仅在于认识论的不同，而是一个更深刻的问题。

在《世界的重新创造》一文中提出，由于中国文化并未有真正的文化移植而导致中国科学的发展注定是不够好的论点，我是完全支持的。其一，截然不同的文化交流和碰撞会给两个文明都带来新的启示。其二，西方的文字系统更适合抽象性思维，而汉语由于其强大的组合能力和良好的直观性导致并未产生新的符号系统对数学进行描述，故而也很难进行复杂抽象的计算与推导。但是笔者认为，关键问题在于，为何中国古代数学与西方数学体系为何没有发生碰撞。从历史时期上来说，中国数学发展和西方数学发展存在一个大的时间差。中国数学的研究发源早，公元三世纪就已经有杰出的数学成果（九章算术最早成书亦是此时，由刘徽编纂成书）。而古希腊数学虽然亦有杰出成就，但是明显影响覆盖的范围远远不到东亚，最多至两河流域，再传入印度境内，而那已经时至公元八世纪。唐宋数学高度发达，并且九章算术逐渐演变为东亚的最重要的数学教科书。而在同时期的欧洲却在经历中世纪，以教会对世界解释权的垄断为主。一直到十三十四世纪时，经由印度，阿拉伯地区将数学原籍传回西欧社会，西方数学才开始发展，然而此时的中国是由蒙古人所统治的时期，数学发展明显受阻。进入十五世纪后，数学在欧洲开始复兴，进入蓬勃发展期，但中国数学却仍不温不火，并且越来越具有偏向性，在这一时期决定了中西方数学的差距。纵观来看，中西方数学发展的断档期对于双方的交流有很强的阻碍，没能在同一时期站在大致相似的高度上形成交流。 从政治上来说，中国古代数学的存在意义实则是为政治服务，所以研究注重实用性，偏向性，对于实际问题的解决很有一套，但是对建立系统性理论没有太大的热情。相较于西方对数学形而上的认识，中国的数学“合为时而用”，是可以“货与帝王家”的才能，如果没有政治支持，那么数学就没有发展土壤。也正因如此，中国的数学家也少之又少，数学文化的传播也并不是随心所欲。重要的，高级的计算技巧是不可能流入民间，自然也不可能催生中国整体上的数学发展。同时，即使在一部分重要的文献如论语，老子，周易等先后传入西方世界，然而东方的数学智慧却未曾到欧洲传播。而从研究方式和工具上，中国数学重视计算，重视实际结果。比如历法上的成就，所依托的正是极高的计算技巧。而这些技巧所依托的符号系统，相较于任何古代数学文明都是先进的。因为简易，而且是组合式的，再通过归纳，简写（比如百，千，万，亿的概念产生，再比如百万，千万，亿万这样的组合概念的产生），我们可以方便直观的表示极多数字，这对计算技巧的研究很有帮助。所以即使西方的符号体系，数字体系传入中国，但是在计算上的优越性必然导致这些不能取代千年沉淀的文字。

而今有很多对比中西方科学发展的探讨，很多的目的在于给中国古代科技科学正名，提振民族自信心，这一点无可厚非，但是我们应本着客观公正的态度探讨。如果将核心观点始终立足于两套文化系统的不同上，进而找到一个平等的平衡点，笔者认为大可不必。无论是以前提出的“倘若假以时日中国也能发展到西方同样程度的科学”，还是现在提出的“中国的科学广义上是格致学，生命博物学”，其实都是在避重就轻地谈问题。且不论西方列强以武力手段打开中国的大门是否是导致中国本土科学流产的原因，就算是在双方互不干涉的前提下，科学的基础学科数学的发展速度就不在一个层次上。中国的数学发展是累积式的，线性的，是稳步发展的，但是西方数学的发展是爆炸式的，好比指数函数，只会发展的越来越快，这就是巨大差距。再有从广义科学角度上切入的观点，基本是上升至哲学层面的认识，不能仅仅停留于探讨不同的思路和想法就长舒一口气，认为找到了平等就可以安心一些。对于现在的学习科学，研究科学的中国人来说，如何汲取古代智慧是非常重要的。这绝不是要抛弃科学的方法论，而是用不同于西方机械唯心论的角度认识世界。值得借鉴的一案便是数学家吴文俊所发展的“吴方法”。吴文俊教授从古代算法思想入手，通过构建程序证明了大量初等几何学，射影几何学内容，取得了非凡的成果。而在科学分支庞杂林立的现代，大体量的科学系统其实反而成了限制人们继续探索的阻碍，如何从中国古代的整体观来认识科学，是一个很可能成功，也极为重要的课题。某种程度上，我们应该庆幸中国的哲学思想与西方并立，或许将带给世界最重要的启示。

微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文

新浪微博：http://weibo.com/duodaa

原文作者： Günter M. Ziegler，柏林自由大学数学教授

翻译作者：donkeycn，哆嗒数学网翻译组成员，华东师范大学博士。

投稿可发至邮箱1178853280@qq.com，详情参见征稿说明。​

微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文

新浪微博：http://weibo.com/duodaa

莱昂哈德·欧拉可能是史上最多产的数学家。欧拉1707年出生于瑞士的巴塞尔，但他一生中的大部分时间都是在柏林度过的。柏林的数学家们都为这一文化遗产而感到自豪。也正因为此，上个月（注：指2016年7月）在这个美丽的城市所举办的第7届欧洲数学大会有欧拉特色也不足为奇了。会上Günter M. Ziegler，一位来自于柏林自由大学的数学家以及公众参与数学的倡导者，作了一个与欧拉有关的五个著名问题的讲座。

这“五个天才的发现”之美，如Ziegler所述，在于，你不必是一个数学家就能去欣赏它们：或许要解决它们是困难的，但问题本身是容易理解且充满乐趣的。这就是为什么我们决定在这里重温它们的原因。

在这里我们不准备过多地谈论欧拉的生平（你可以在“MacTutor数学史档案”（注：原文“MacTutor History of Maths archive”）这个网站以及各种各样关于欧拉的书中找到许多有趣的信息）。值得说的是，欧拉也在俄国的圣彼得堡度过了很多时光。在那里，他育有13个孩子，在失明后完成了毕生大半的工作，并于1783年去世。欧拉曾声称“他作出一些最伟大的数学发现的时候，同时会抱着一个婴儿在他的怀里且其他孩子会围在他的脚边玩”。可悲的是，其中只有五个孩子活到成年。

现在让我们把欧拉的生平放在一边，回到那五个著名的问题上来。（这里没有注明问题的详情，有兴趣的可以百度之）

哥尼斯堡七桥问题  

是否可以在该市的地图上找到一条路线，使得穿过每一座桥恰好一次？欧拉对这个问题的解答导致了图论的起源。

骑士遍历问题

是否可以连续移动一个骑士（注：骑士指国际象棋中的“马”），使得它经过棋盘上每个格子恰好一次，最后回到初始格子？欧拉是第一批系统地分析这个问题的人，但仍有一些相关问题至今还是开放的。

36军官问题

欧拉可能没有完全解决这个问题，但它导致了许多重要的工作，包括我们今天知道的数独。（编者注：36军官问题是问，从不同的6个军团各选6种不同军阶的6名军官共36人，排成一个6行6列的方队，使得各行各列的6名军官恰好来自不同的军团而且军阶各不相同，应如何排这个方队？）

欧拉多面体公式

这个关于三维物体的令人惊讶的结果告诉我们一些关于空间本质的东西。（编者注：欧拉多面体公式是指，任何简单多面体的顶点数V、棱数E及面数F间有关系V - E + F = 2）

巴塞尔问题 

这是一个无穷和，困惑了不少著名数学家，直到欧拉找到了令人惊讶的答案。

微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文

新浪微博：http://weibo.com/duodaa

原文作者：高尔斯，剑桥大学数学教授，1998年菲尔兹奖得主。

翻译作者：radium，哆嗒数学网翻译组成员，就读于重庆第二师范学院。

投稿可发至邮箱1178853280@qq.com

微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文

新浪微博：http://weibo.com/duodaa

已经有一段时间了，自从我在“哲学点滴”条目下写了一个帖子，也是在那儿我提出了像“如何说明一个命题比另一个命题更强，或者两个命题是等价的？”这样的问题。这篇文章就是讨论这个在我脑海里思考了很久的问题，但我发现它比我预想的更难。

似乎可以将定理分为三种类型：一种是不需要运用反证法来证明的，一种是不管用不用反证法都能证明的，最后一种是似乎只能用反证法。但是如何把一条定理归为这三种类型中的一种呢？

这个问题源自于我教给学生们一种前人所想出来的证明方法。比如下面这个“假设数列(An)发散。由此可知...几行计算...这意味着An→A，矛盾”，当你指出这个证明的第一行和最后一行可以被删除时，他们有时会十分惊讶。

没那么荒谬的证明更多的是像这样的。“我们知道|y-x|<δ，假设|sin(y)-sin(x)|≥δ，因为sin导数的绝对值最大为1，它推出|y-x|≥δ，这与条件矛盾。所以|sin(y)-sin(x)|<δ”在这个证明中，显然更好的是直接从前提出发，通过引理|f(x)-f(y)|≤sup|f’|·|x-y|推导出|sin(y)-sin(x)|<δ。但是，通常是运用反证法来证明引理：假设这个结论是错误的，然后运用中值定理。

所有这一切的结果是，已有的形式无法给我什么提示，“如果你的定理是像这样的，那么尝试着用反证法，不然不要这样做”对于本文的剩余部分，我将讨论另外一组例子，来阐释问题的复杂性。

例1： 根号2的无理性

这当然是运用反证法的经典证明，我们甚至可以给出一个证明这个命题必须要使用反证法的“准证明”。因为“无理性”意味着“对于任何整数对(p,q)，都无法使sqrt(2)（sqrt表示开根号，下同）与p/q相等”。如果这是定义，那么让我们假设证明的最后两行消失了：因此sqrt(2)有性质P，因此sqrt(2)是无理数。

于是我们会问“为什么有性质P意味着那个数是无理数？”这可以很明显的看出来性质P意味着无理性，但是为了证明它仍然有必要说“于是，取任意有理数x=p/q...因此x没有性质P”（为什么这个是有必要的呢？正是出于同样的原因！也许这是证明长度或其他类似东西的归纳）

带着这些问题，考虑以下论证，我们从计算sqrt(2)的连分数展开开始。于是我们得到sqrt(2) = 1 + ( sqrt(2)-1 ) = 1 + 1/( sqrt(2) + 1)。继续对分数的分母进行展开得到2 + ( sqrt(2)-1 ) = 2 + 1/( sqrt(2)+1 )，于是我们看到连分数展开开始出现循环，标准记法是[1;2,2,2,……]。特别是,它是无穷的,因此sqrt(2) 是无理数。

第一眼看这个证明的，这似乎就是直接论证而不是运用反证法证明的：我们运用假设演绎出具有明显的无理数性质。但是，就像我之前笼统的评述一样，一个潜在的问题就是“为什么一个具有无限连分数展开的数是无理数？”

答案是什么呢？很明显一个有理数是有限小数，因为当你计算的时候，它的分母不断减少...哎呦，不好意思，这又是一个反证法。

所以答案也许应该这么说，如果你正在试图证明一个否定性的命题，那么你就不得不用反证法，但是什么是“否定性命题”呢？以下的定理如何？

定理：如果p和q是整数，那么p²≠2q²

啊哈！你说，是因为“不等于”形成了否定。但我们可以通过快速的变形成来解决。

定理：如果p和q是整数，那么(p²-2q²)²>0。

这个的否定又是怎样的?如果你认为它不管怎么样都受限于“严格大于”的概念，那么下面这个又怎么样？

定理：如果p和q是整数，那么存在实数x使(p²-2q²)²x = 1。

对我来说，这个命题起来对是相当肯定的，因为它断言某种存在性。

但如果你思考一下如何证明样的x存在，它将变的没那么肯定了。显而易见的想法是：“唯一可能出错的地方在p²=2q²上面，所以我们只须证明p²≠2q²。”那它又是否定的了。所以这是否意味着，如果对于一个命题，证明它的唯一合理的方式是将它重新归纳为一个包含否定词“非”的命题，那么这个命题就是否定性命题？即使这样看起来是正确的，似乎也很难具体化。

这儿还有一个对于最后一个类型的例子。无限是一种无理数性质吗？有人可能说是的，因为它意味着不是有限。但是，当我们讨论到连分数时，我们关心的是序列，我们可以定义一个无穷序列，如果它的项可以和自然数之间建立双射。（我们也可以定义一个无穷集合，如果它和它的某个真子集之间可以建立单射。但是仅仅由于真子集没有包含全部元素，我们就能称真子集是一个否定性的概念吗？）

例2.有界闭区间上的连续函数

直到最近我才“知道”下面是这种实例。如果你想运用[0,1]的紧性证明什么东西时，那么你既可以直接使用海涅-波莱尔定理（Heine-Borel theorem ），也可以通过反证法来处理，具体就是把区间内的数重新排成序列并应用波尔查诺-维尔斯特拉斯定理（Bolzano-Weierstrass theorem.）。

例如，证明连续函数f在区间[0,1]是有界的，你既可以通过找函数f在每一点的领域是有界的（由连续性的定义）且将区间[0,1]有限覆盖（运用海涅-波莱尔定理），也可以假设函数f是无界的，构造序列(xn)，满足对任意n有f(xn)≥n，应用波尔查诺-维尔斯特拉斯定理通过反证法来证明。

我也默认有一种算法能将一种证明转换为另一种证明，虽然我从来没有实际尝试过其中的细节。

但是最近，在我和一个同事的谈话的过程中，谈到了下面关于这个定理的证明。在此之前我一直认为于自己对证明怎么运行的理解的很到位，但下面这个证明让我意识到事情远不止那么简单。这个想法是尽量模仿上述反证法的证明，但是最后的结果并没有用到矛盾来证明。具体的讲，构建一个序列是最有可能的引起矛盾的序列，然后证明它不会引起矛盾。下面是论证的具体内容。

令S∈R∪{∞}是{f(x) : x∈[0,1]}的上确界。通过上确界的定义，我们可以找到一个序列(xn)使f(xn)→S，通过波尔查诺-维尔斯特拉斯定理选择一个收敛的子序列yn，我们得到(f(yn))是(f(xn))的子序列，所以f(yn)→S。但是如果y是序列(yn)的极限，且f(yn)→f(y)，所以S=f(y)，即f(y)是函数f的一个上界。（注意这个证明也表明这个上界可以取到。）

似乎这个证明没有涉及矛盾。但是如果我们进一步思考，你会发现矛盾隐藏在证明的“明显”步骤中。例如，我们怎么知道我们可以找到一个序列(xn)使f(xn)→S？我们需要将它划分为两个问题（除非我们想要定义隐含在其中的广义实数直线的拓扑）。

S∈R不是值得深究的问题，因为它，我们立刻知道函数f是有界的。（尽管这一步是没有必要的，我们也可以获得其他的信息，比如函数f达到了上限）。如果我们将问题转向为S=∞，我们正在做的证明与假设函数f是无界的有什么不同？我自己也很困惑。

最后的感想

从这些例子中反映出来的一件事是，反证法的概念与你用的定义和你认为理所当然的一些小结论有关。例如，我们定义一个数是无理数，如果它的连分式展开是无限的。事实上我不会主张这样做，但如果有人这样做，那么我给出的根号2的无理性“直接”证明就是直接的。而且如果我们不准使用假设|f(x)-f(y)|≤sup|f’|·|x-y|那么要证明在|x-y|<δ的情况下|sin(y)-sin(x)|<δ就会变得没那么直接，还是需要反证法。

在这种情况下，也许我该给这样答复学生，虽然上面的讨论还是不很明确，但已经尽力了。——反证法是一个非常有用的工具，但是尽量不要使用它，除非你不得不用它。

微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文

新浪微博：http://weibo.com/duodaa

微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文

新浪微博：http://weibo.com/duodaa

就在我们国人愉快的欢度春节的这段时间，美国总统特朗普又搞事情了。

1月27日，也就是大年三十这天，特朗普签署了“关于难民和移民政策的行政命令”，宣布暂停美国难民项目4个月，暂时禁止伊朗、伊拉克、利比亚、索马里、苏丹、叙利亚和也门的公民入境美国，为期90天。由于所点名的七个国家都是穆斯林国家，所以这个行政命令被俗称称为“穆斯林禁令”。

这个行政命令引发了美国国内和国际社会的强烈争议，其中不乏激烈的反对。而在竞选时期就和特朗普不和的学术界的一些“大佬”，也加入反对“穆斯林禁令”的队伍中。他们建立了一个网站（https://notoimmigrationban.com）联合学术界的学术人签名反对特朗普的这个行政命令。

这个网站上，他们对特朗普的“穆斯林禁令”表明了三条主要态度：

1、 这个行政命令是歧视性的。

2、 这个行政命令对美国的国家利益有害。

3、 这个行政命令是强加于我们学术界的过分负担。

目前，在该网站上已经有超过27000名人士签名，其中美国教员超过20000名。签名者中，很多是学术界的顶级大咖——51名诺贝尔奖得主、104名学术界其它重要奖项得主（包括菲尔兹奖、狄拉克奖、克拉克奖、图灵奖、庞加莱奖、科学突破奖、普利策奖、麦克阿瑟天才奖）。

其中菲尔兹奖得主11位，他们是：

德利涅，1978年菲尔兹奖得主，就职于普林斯顿高等研究院，出生于比利时。

德里费尔德，1990年菲尔兹奖得主，就职于芝加哥大学，出生于前苏联时期的乌克兰。

高尔斯，1998年菲尔兹奖得主，就职于剑桥大学，出生于英国。

林登施特劳斯，2010年菲尔兹奖得主，就职于希伯来大学，出生于以色列。

麦克马伦，1998年菲尔兹奖得主，就职于哈佛大学，出生于美国。

米尔扎哈妮（女），2014年菲尔兹奖得主，就职于斯坦福大学，出生于伊朗。

奥昆科夫，2006年菲尔兹奖得主，就职于哥伦比亚大学，出生于前苏联时期的俄罗斯。

陶哲轩，2006年菲尔兹奖得主，就职于加州大学洛杉矶分校，出生于澳大利亚。

弗沃特斯基，2002年菲尔兹奖得主，就职于普林斯顿高等研究院，出生于前苏联时期的俄罗斯。

威藤，1990年菲尔兹奖得主，就职于普林斯顿高等研究院，出生于美国。

泽尔曼诺夫，1994年菲尔兹奖得主，就职于加州大学圣迭戈分校，出生于前苏联时期的俄罗斯。

不难发现，签名反对这个命令的菲尔兹奖得主绝大部分都是出生于美国国外而在美国就职的学者。在中国人气极高的华裔数学家陶哲轩出生于澳大利亚，而历史上第一位女性菲尔兹奖得主米尔扎哈妮，就来自“禁令七国”中的伊朗。

历史上看，数学学术活动也有受政治影响的先例。比如由于前苏联政府的限制，1970年得主诺维科夫和1978年得主玛古利斯没能前往颁奖地领奖（颁奖地点分别是法国和加拿大），而1966年得主格罗滕迪克也抵制了在前苏联举行的菲尔兹奖颁奖典礼，以抗议当时苏联在东欧的军事行动。

微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文

新浪微博：http://weibo.com/duodaa