为什么在等公交车时,要等的车总还没有来？

作者：小米，哆嗒数学网群友。

 

关注 哆嗒数学网 每天获得更多数学趣文

 

 

概率是数学里刻画随机性的一个有力工具。借助概率模型，我们可以严格地讨论像“将一枚硬币随机抛起，得到正面或反面的概率为多少”这类随机现象。

 

很多时候，概率可以用数学公式准确地表述我们一些直观的感觉。例如，对于“今天是阴天，所以更有可能下雨”这个论断，我们就可以借助概率中相关性的概念来理解。

 

但是有的时候，如果仅从直观上对“随机性”进行理解而不经过严格的数学推理，却可能导出一些错误的结论。例如有名的“伯特兰悖论”：考虑一个内接于圆的等边三角形。若随机选圆上的弦，则此弦的长度比三角形的边较长的概率为多少？伯特兰提出了三种“随机”选取弦的方法，却导出了不一样的结论。

 

“伯特兰悖论”说明，在用概率处理问题时，我们需要明确随机性是如何产生的。这个过程的严格化是由柯尔莫格洛夫的概率论公理化解决的。并不是所有的“随机性”都能够在数学上站得住脚。例如，在1到10之间随机（等概率地）选取一个整数是可以做到的，而从全体自然数中随机（等概率地）选取一个整数则是不可能的。

 

今天我们要讨论的问题也是一个乍看上去与直觉相悖的例子。假设有一路公交，每班车发车间隔有50%的机率是10分钟，有50%的机率是20分钟。现在你到家楼下的车站坐车，又假设每分钟有一名乘客到达车站等车，那请问当你上车时，乘客排队的平均队伍长度是多少？

 

直觉上答案应该是(10+20)/2=15。理由如下：由于乘客到达的速率恒定，所以上车时队伍的长度与你坐上的车的发车间隔成正比；由于发车间隔有50%的概率是20分钟（对应队伍长度20人），有50%的概率是10分钟（对应的队伍长度为10人），所以平均下来应该是20和10的平均数，即15人。

这个论证有没有问题呢？我们把问题适当抽象一下，也许可以看出一点端倪。假设发车间隔以50%的概率为a，50%的概率为b，那么按照前面的论证，平均队伍长度应该是(a+b)/2。但是，我们可以考虑一种极端情况，就是a很小而b很大的情况。比如假设a是1秒钟，b是1小时。这样，我们可以把相隔一秒钟的两辆车几乎认为是“同时”到达的。那么我们就面对着如下的情况：很多辆车可能一起到站，但是下一次有车隔1个小时。在这种情况下，因为我们很难刚好碰上有车到站的时刻，队伍的长度其实会是1个小时的队伍，也就是b。

 

那么为什么直觉带来了错误的答案呢？原因是我们混淆了“平均发车间隔”与“平均等车时间”这两回事。虽然它们都是一个随机的时间长度，但是里面的随机性是不一样的！

一班车的时刻表可以用下面这张图来刻画。我们把数轴分割成一些首尾相接的区间。区间有两种：一种是较长的蓝色区间，代表发车间隔为b；一种是较短的红色区间，代表发车间隔为a。区间的端点代表着公交车到站的时刻。

 

那么两种随机性分别是指什么呢？当我们说“发车间隔随机地选取a或b的时候”，随机地用两种长度的区间来分割数轴，也就是说，当我们选取一段很长很长的时间来观察的时候，里面出现的红区间和蓝区间的数目各占约50%。而当我们讨论“平均等车时间”的时候，我们是在数轴上任取一点，考察它是落在红区间上还是落在蓝区间上。

 

但是，因为蓝区间比红区间要长，所以即使红区间和蓝区间的数目“大致相等“，我们”随机“选取一个点还是更可能落在蓝区间中。这导致了在计算”平均等车时间“的时候，红区间与蓝区间出现的概率改变了！

 

更具体地说，在这个例子中，因为红区间长为a，蓝区间长为b，所以在它们的数目为1:1的情况下，占据的时间长度大概为a:b。因此在计算“平均等车时间“的时候，红区间出现的概率为a/(a+b)，而蓝区间出现的概率为b/(a+b)。所以最后的平均等车时间为

 

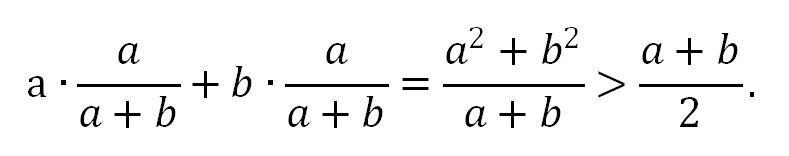
当然，这里我们计算的“平均等车时间“其实是队伍里排队最久的人所等待的时间（在我们的设定下这就是队伍的总长度）。如果我们只是随机地到达车站，那么可以想象平均来说，我们将会排在队伍的中间，因此我们的真实等待时间其实只有上面计算结果的一半。

 

上面的论证过程也有一些不够严格的地方。其中之一就是如何定义“随机“在数轴上选取一个点。为了解决这个问题我们需要转换思维。我们把班车到达的时刻看作是一个实数上随机的点集，满足相邻的两点之间的距离随机地为a或b，并且还具有某种时间上的“均质性”，数学上也叫“平稳性”。这时，我们也不需要去抽取数轴上任意一个点，而只需要固定一个点，例如原点，考察原点所在区间的长度。由于时间上的均质性，任意固定点都是一样的。从一个平稳的点过程出发，在一个固定点去观测会得到特别的统计结构，这就是帕姆—辛钦(Palm—Khinchin)理论。简单地应用在我们的等车例子中，假设发车间隔的分布具有密度函数ρ(x)，那么原点所在区间的长度具有密度函数正比于xρ(x)。这里的因子x表明长度越长的区间越有可能被我们观测到。

 

这个例子也说明了，观测结果有时候会影响观测过程，比如在这里，较长的发车区间增加了我们观测到它的概率。这和“幸存者偏差“的产生有着同样的逻辑。当我们很久等不上车，这并不是因为我们自己特别倒霉，而是从理论上，人就更可能花更长时间等车。也许呢，生活中的不顺也并没有我们想象的那么多。

 

 

关注 哆嗒数学网 每天获得更多数学趣文