化圆为方：数学家从没停止研究，只是不是原来的样子

本文编译自量子杂志网站

原文作者：Steve Nadis

编译作者：Math001

 

 

关注 哆嗒数学网 每天获得更多数学趣文

大约公元前450年，安那克萨哥拉斯终于有了静下来思考的时间。这位哲学家兼数学家的古希腊人声称太阳不是神，而是和罗奔尼撒半岛一样大的炽热岩石。安那克萨哥拉斯因此被打入大牢。作为信奉“理性统治世界”的哲学家代表，他在狱中着手思考解决一个数学问题。这就是著名的化圆为方问题：用圆规和无刻度的尺子作一个和已知圆一样大的正方形。

 

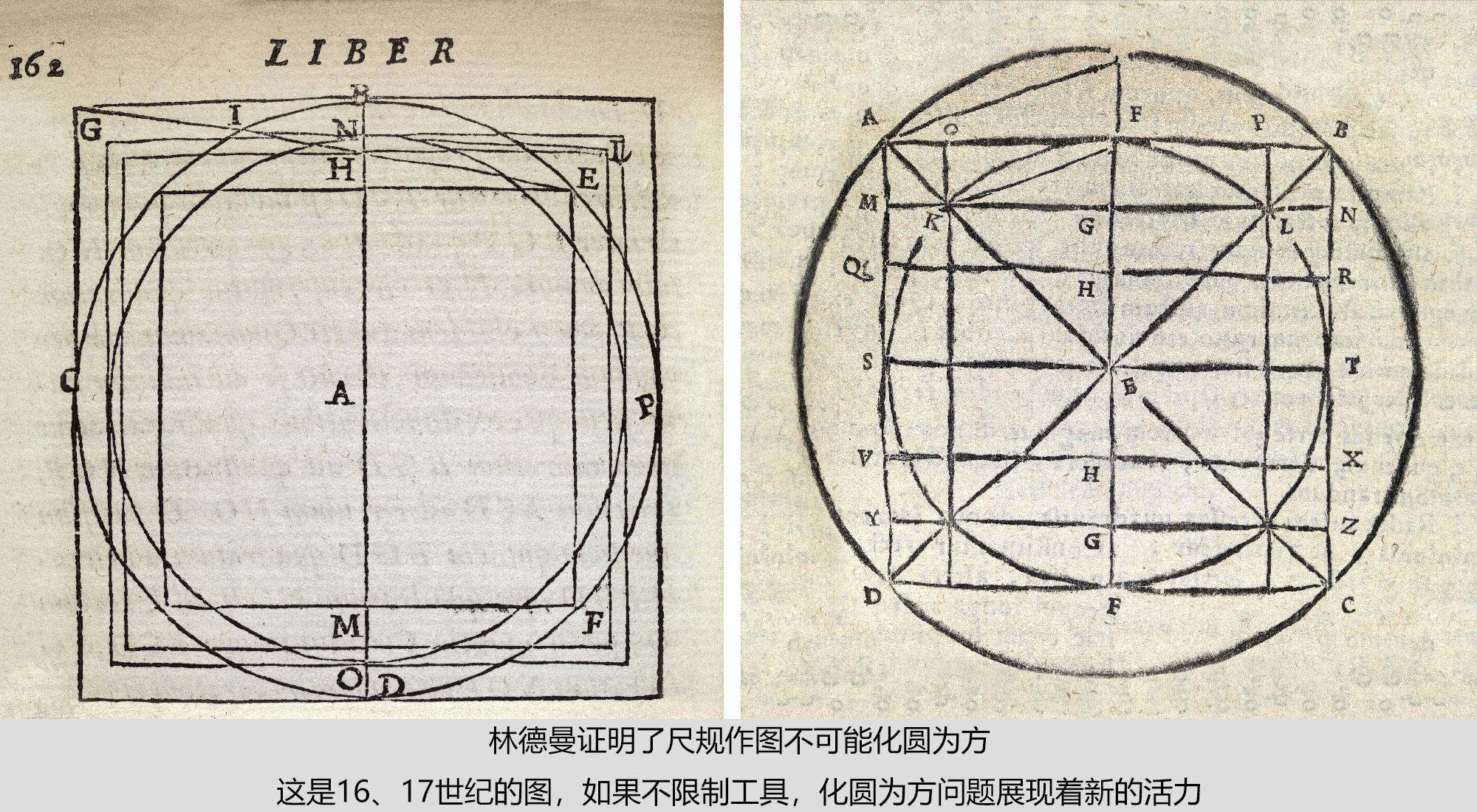
安那克萨哥拉斯的本来的那个问题其实在1882年就解决了。德国数学家林德曼用一套经典方法证明了尺规作图化圆为方是不可能的。他证明了圆周率π是超越数。但是尺规作图是不可能做出超越数的线段长度的，所以证明了问题的不可能性。

 

问题并没有因此终结，意外的是，数学家们还在这个问题上工作着。1925年数学家塔尔斯基唤醒了这个问题，他修改了原始问题的规则：如果把圆分成完全相同的有限多块，这些小块是否能重新拼成一个面积相同的圆呢？这样的问题有个统一的名字，叫做等体分解。

 

 

 

 

 

 

 

 

 

换句话说，如果两个物体可以分解成大小和形状完全同部分，那么这两个物体就是同等体分解的。更精确的说，如果两个物体能分解成有限多个部分，每个部分完全一致，那么就说这两个物体就是同等体分解的。

 

 

 

1964年的一篇论文让塔尔斯基版本的化圆为方问题有了第一次实质性的进展。论文的结论是，用剪刀是无法完成化圆为方的等体分解。着意为着，如果要解决这个问题，可能需要把圆分解成更复杂的分型：一种可能布满小洞或者无限锯齿的形状。

 

 

1990年，数学家拉茨科维奇(Miklós Laczkovich)响亮的从正面解决了塔尔斯基的问题：塔尔斯基的化圆为方问题是成立的。

 

 

 

拉茨科维奇证明的是，用一种复杂和非常规的图形对圆进行分解，用不超过10的50次方个小块进行移动(连旋转都不用)，这些小块就能重新拼成正方形。

 

 

但是拉茨科维奇不直接操作几何图形而得到这个结果的。实际上，他把原本的几何问题转化成了图论问题。用两个顶点集合，一个集合对应圆，一个几何对应正方形，然后之间建立两个顶点集合之间的一一对应关系，从而完成的证明。

 

有数学家认为，拉茨科维奇的结果让人“瞠目结舌”，拉茨科维奇的向大家展示了如何“把一个圆的掰成直的”。

 

 

拉茨科维奇的证明还有一个瑕疵。这个证明是存在性证明，在数学界被称为“非构造性证明”。他证明了事情可以办到，但没有给出分解的具体办法来说明如何办到。更让人不爽的是，分解的小块是“不可测的”，这意味着这些小块的面积不存在。

 

 

几十年后的2016年，格拉博斯基(Łukasz Grabowski), 玛斯(Andras Máthé) 以及皮胡尔科(Oleg Pikhurko)共同撰写的论文让这个问题又有了重大进展。和拉茨科维奇的论文不同，证明几乎是构造性的，就是说分解的每一个小块都有明确的描述。但还是有一个瑕疵：把圆分解成的小块并没有填充满正方形的全部，还有很小很小的一部分没有填充。这没有填充的部分面积是零，数学家称为“零测度集”。

 

尽管还是没做到完全覆盖，但也是这个问题的重大进步——除了一个零测度集合，我们按塔尔斯基的规则成功的用构造性的方法化圆为方。

 

 

一年后，加州大学的马克斯( Andrew Marks)和多伦多大学的安格(Spencer Unger)在这个问题上有取得重大进展，他们第一次用完全构造性的方法证明了塔尔斯基版本的化圆为方——而且是完整的拼成，没有任何多余部分。论文完整描述了如果把圆分成小块，然后重新拼成一个等体积的正方形，不再有多余的零测度集合。

 

 

这一次分成的小块更多，需要大约10的200次方块，每一个小块的结构依然很复杂。论文作者认为，这是一个缺陷，因为这些小块要站在数学家的立场才能理解，很难用形象的方式展示出来。

 

 

这就留下了改进的空间，用更少数量的小块，或者更简单的形状的小块。数学家并没有停止探索，他们已经用计算机做了一个实验，据说22块就可以，但目前还没有给出这个的证明。

 

关注 哆嗒数学网 每天获得更多数学趣文