原文作者：John Baez。

译文作者：豆浆，哆嗒数学网翻译组成员，数据分析师。

校对：donkeycn。

 

 

微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文

新浪微博：http://weibo.com/duodaa

 

 

开普勒问题涉及一个质点在引力作用下运动，就像是一个行星围绕太阳运动。牛顿证明了假设它不飞向无穷远，这种粒子的轨道是一个椭圆。有很多方法可以证明这一点，但最富于启发性的想法是将轨道想象成4维空间里的一个圆。当这个圆投射到3维空间上，它就会变成一个椭圆。

 

 

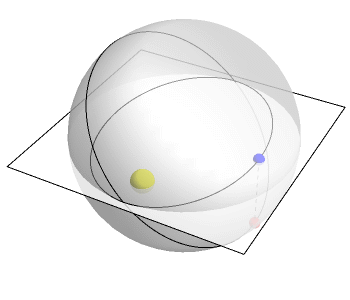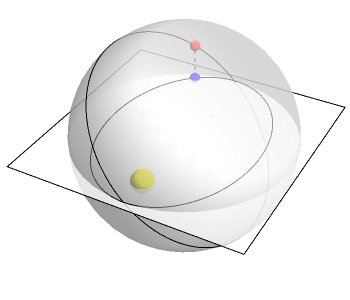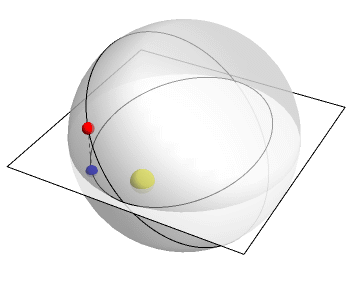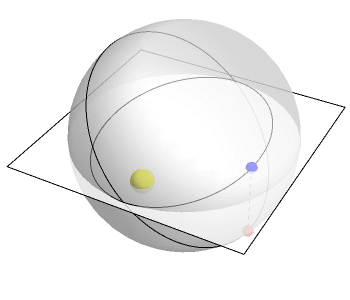
Greg Egan创建了上面的动画来展示这一过程。这个平面代表我们住的3维空间里的2维，垂直方向代表了第四维。一个点在R^4绕了一圈。但是将这个圆投射到R³，我们就会得到一个椭圆：行星的实际轨道。

 

什么是第四维？它与时间有关，但不完全是时间。它是常规时间和一个时间的重新参数化版本之间的差，该时间的流逝速度与行星到太阳的距离成反比。

 

动画使用了这个另类的时间。相对于这个时间，行星正在以恒定速度在4维空间上做圆周运动。但在普通时间下，当它接近太阳时，正如行星必须要做的，就是其在3维上的投影运动得更快。

 

至少从1980年以来物理学家们就知道了这个观点，这得益于由数学物理学家Jürgen Moser写的一篇论文。这个故事的某些部分是老得多。许多论文也已经有写到，但这一次是特别优雅：

 

Jesper Göransson，开普勒问题对称性，2015年3月8日。

 

关于描述行星运动的Göransson 4维空间的最好的事情是，它给出了一个惊人的事实，一个干净的解释。你可以取任何椭圆轨道，施加一个4维空间的旋转，并获得另一个有效的轨道！

 

当然，我们可以在通常的3维路径下围绕太阳旋转一个椭圆轨道并得到另一椭圆轨道。有趣的是，我们还可以做4维旋转。这样可以使一个丰满的椭圆看起来瘦小：当我们将一个圆倾斜到第四维，它在3维空间的“影子”变得更瘦！

 

事实上，你可以通过这样的一个四维旋转把任何椭圆轨道变成任何其它具有相同能量的椭圆轨道。所有具有相同能量的椭圆轨道都是四维空间里在同一球面上的圆形轨道的投影！

 

让我们来看看更多关于数学方面的细节。

 

开普勒问题

 

 

假设我们有一个质点在平方反比定律的作用下运动。其运动方程为

 

 

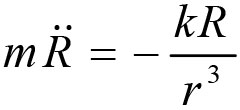
其中R是它作为时间函数的位置，r是从原点的距离，m表示它的质量，而k是表示力有多强。由此我们可以得出能量守恒定律，如下

 

 

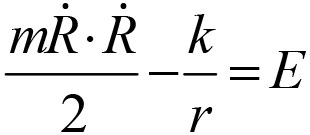
对于一些常数E，它依赖于粒子轨道，但不随时间变化。

 

 

让我们考虑一个引力，因此k>0，而且是椭圆轨道，因此E<0。让我们把这个质点称作一个'行星'。这是一颗围绕太阳运行的行星，在这里我们把太阳看得非常重以至于它完美地保持固定在原点。

 

 

让我们把注意力集中在一个具有单一固定能量E的轨道上.这可以让我们自由地选择质量，长度和时间的单位

 

 

 

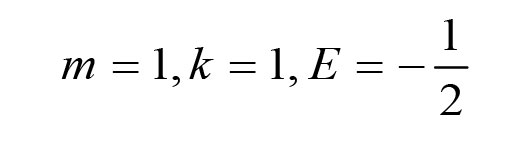
这将减少一堆杂乱的字母，使我们专注于关键的想法。如果您更希望看到技术细节方面的东西，那就去看看Göransson的论文吧。

 

现在运动方程变成了

 

 

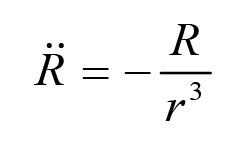
能量守恒方程变成了

 

 

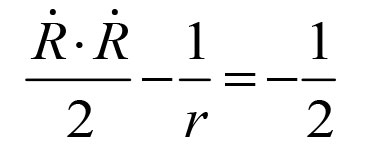
显然是由于Moser，这个伟大的想法是从普通的时间概念切换到一种新的时间概念！我们将这个新的时间叫做s，并要求

 

 

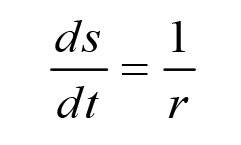
你离太阳越远，这种新的时间走得越慢。因此，当行星远离太阳时，使用这种新的时间会加快它的运动。如果这看起来是倒退的，思考一下吧。对于一个离太阳很远的行星，这个新时间的一天可以等于普通时间的一周。所以，使用新时间来测量，一个远离太阳的行星可以运行一天，而这通常需要一周的时间。

 

当它远离太阳时，这弥补了行星运行得很慢的正常倾向。事实上，用这种新的时间，当行星离太阳最远和最近的时候，它运行得一样快。

 

随着这新的时间概念，令人惊奇的事情发生了！为了看到这一点，首先使用这一新时间概念改写能量守恒定律。沿用牛顿的记号，我们一直在使用点表示普通时间的导数。让我们使用上撇符号(′)来表示相对于s的导数。因此，例如，我们有

 

 

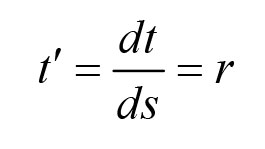
和

 

 

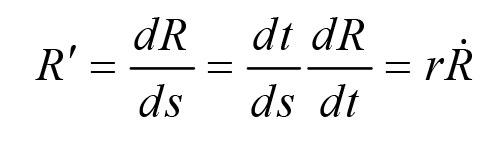
使用这种新的时间导数，Göransson证明能量守恒可以写成

 

 

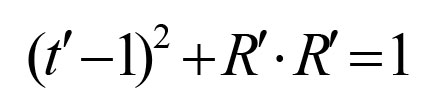
这是4维空间的一个球面方程！

 

稍后我们就会明白为什么能量守恒定律可以这样写。首先让我们来谈谈这意味着什么。要理解它，我们应该把普通的时间坐标t和空间坐标（X，Y，Z）平等看待。点(t,x,y,z)随着参数s的变化在4维空间移动。我们现在看到这个点的速度，即是v=(t′,x′,y′,z′)

 

在4维空间里的一个球面上移动。它是以点(1,0,0,0)为中心的半径为1的球面

 

在进一步的计算之后，我们可以得到一些其他精彩的事实：

 

 

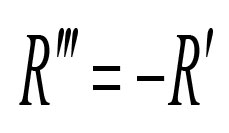
和

 

 

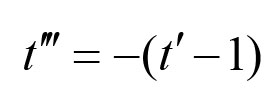
这些是谐振子的普通方程，但加入了一个额外的导数。

 

这些事实证明如下。首先，让我们思考一下他们意味着什么。我们可以按如下说明用文字表达这些事实：4维的速度v进行了关于点（1,0,0,0）的简谐运动。

 

那很漂亮。但由于v还停留在以这个点为中心的单位球面上，我们可以得出更好的结论：v必须以恒定的速度沿着这个球面一个大圆移动！

 

这意味着4维速度的空间分量的均值为0，而t分量的均值为1。

 

这里的第一部分有很大的意义：地球永远不会从太阳漂移得更远，所以它的平均速度必须为零。第二部分是有点微妙，但它也有道理：普通时间t关于新的时间参数s以平均速度1向前移动，但其变化率是正弦振荡的。

 

如果我们对方程R'''=-R 的两边积分，我们会得到

 

 

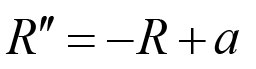
对于某个常数矢量a。这就是说位置R关于一个点a谐波振荡。由于a不随时间变化，这是一个守恒量：它被称为龙格 - 楞次矢量。

 

人们常常从平方反比力定律入手，证明角动量和龙格 - 楞次矢量是守恒的，并使用这6个守恒量和诺特定理证明存在一个6维对称群。对于具有负能量的解，这正是4维空间的旋转群，SO(4)。随着越来越多的工作，我们可以看到开普勒问题是如何与在4维空间的谐振子相关的。这样做涉及到重新参数化时间。

 

在很多方面来说，我更喜欢Göransson的做法，因为它坚持从重新参数化时间入手。这让他更有效地证明，行星的椭圆轨道是四维空间中的圆轨道在三维空间的投影。四维旋转对称性是那么明显！

 

实际上Göransson在n维空间里用平方反比定律进行论证;这没有更困难。n维的椭圆形轨道是n +1维圆形轨道的投射。角动量是n维的二重向量;它与龙格-楞次矢量一起形成在n + 1个维的二重向量。这是与这个问题的第（n+ 1）维的旋转对称相关联的守恒量。

 

他还证明了对于正能量的双曲线形轨道和零能量的抛物线形轨道也有类似的结论。双曲线的情况下有洛仑兹群对称性，而零能量的情况下有欧几里德群对称性！这是已知的，但很高兴地看到Göransson的计算是如何轻松地处理所有这三种情况。

 

 

数学细节

 

用矢量微积分检查所有这一切是一个简单的练习，但它需要一些工作，所以让我在这里做了一些。仍然会有细节留待填补，我希望你可以试一试。

 

请记住，我们的时间重新参数化给出了

 

 

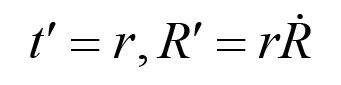
其中上撇符号(′)代表d / ds。因此，我们可以从能量守恒入手：

 

 

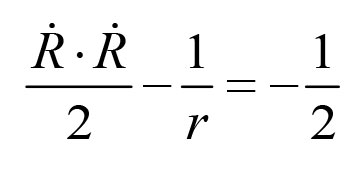
并且使用

 

 

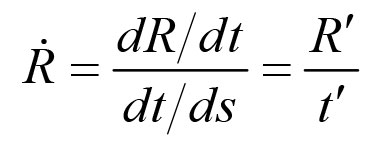
（译者注：原文可能有误，根据上文，这里应该是 ）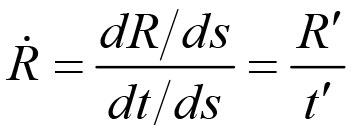

 

得到

 

 

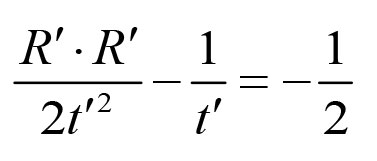
运用一点代数知识给出

 

 

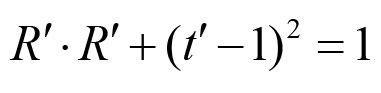
这证明了4维速度v=（t’，x’，y’，z’）在中心为（1，0，0，0）的单位球上。

 

下一步就是取运动方程

 

 

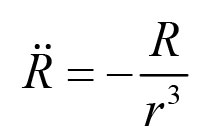
并采用上撇符号(′)（s的导数），而不是点（t的导数）重写。我们先从

 

 

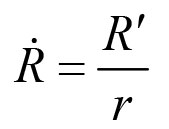
并再次微分得到

 

 

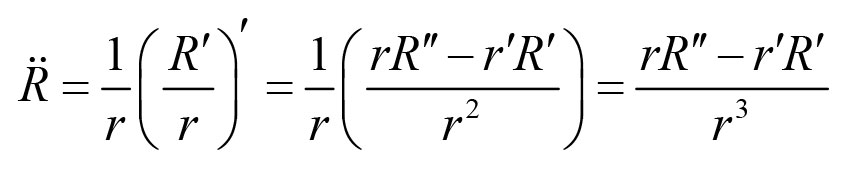
接下来，我们其他的方程为R''给出了

 

 

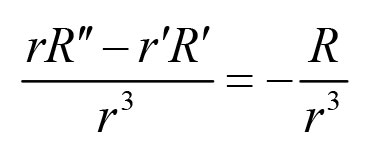
或者

 

 

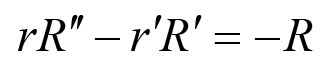
因此有

 

 

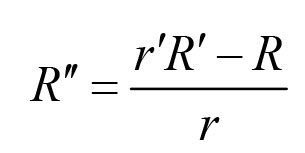
为了走得更远，这也是为了给R''得出一个很好的公式。首先我们计算

 

 

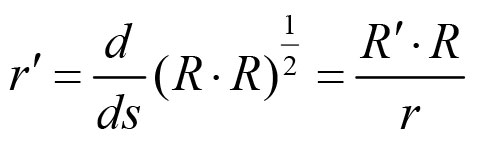
然后再微分

 

 

 

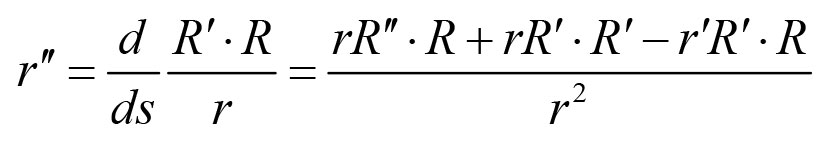
给R''代入公式，会出现一些精彩的相消，我们得到

 

 

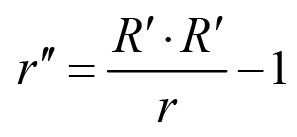
但我们还可以做得更好！记住了，能量守恒有

 

 

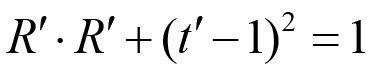
而且我们知道t'=r .因此,

 

 

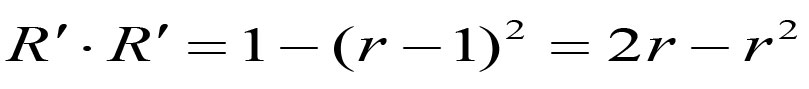
和

 

 

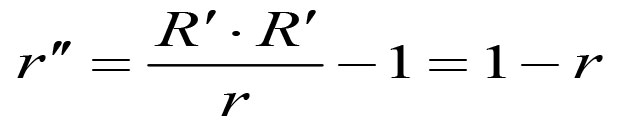
所以，我们知道

 

 

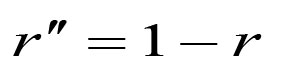
因为 ，如预期的给出了

 

 

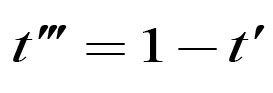
下一步让我们给 得到一个类似的公式。我们先从

 

 

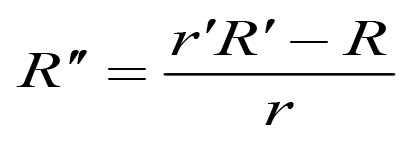
入手，然后两边微分，得到

 

 

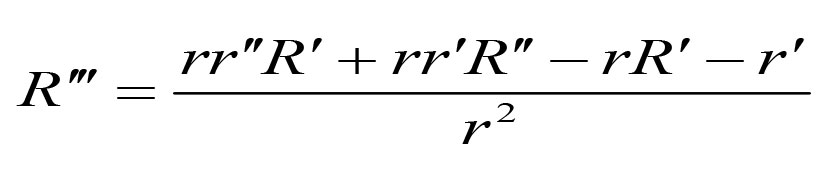
然后给r''和R''代入我们的公式。 出现了一些真正的神奇的相消，然后我们如预期得到

 

 

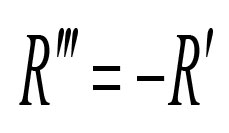
公式两边积分，我们就得到了

 

 

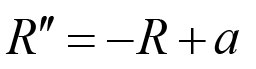
对于一些固定的矢量a，龙格 - 楞次矢量。这是说R进行了关于a的谐波运动。这是相当了不起的，R和它的范数r都进行了谐波运动。

 

 

微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文

新浪微博：http://weibo.com/duodaa